5.1 – Capire l’approccio recreaMATHS

Quindi, cos’è un “approccio recreaMATHS”? Come possiamo ricreare l’approccio nell’apprendimento della matematica nella scuola materna?

In questo capitolo, daremo risposte alle domande di cui sopra e cercheremo di spiegarvi in modo più approfondito l’approccio recreaMATHS. Parte dell’approccio recreaMATHS si basa sulla più ampia competenza matematica nella scuola materna. Considerando come un bambino impara in generale, possiamo determinare un modo su come insegnare la matematica ai bambini della scuola materna. Gli insegnanti possono identificare approcci di insegnamento che evitano la pressione eccessiva e e gli atteggiamenti negativi verso il processo di apprendimento di un bambino. L’apprendimento è uno sviluppo complicato, in cui ogni singolo bambino impara in modo diverso ed evolve questo apprendimento al proprio ritmo. Ci sono molti aspetti coinvolti in questo processo, tuttavia, tutti i bambini condividono un cervello e un corpo in via di sviluppo, e possono essere notevolmente influenzati dalle loro esperienze – sia sociali che culturali – che possono aiutare nel processo di apprendimento (Gifford, 2005).

L’apprendimento può essere considerato come un ” lavoro carico di emozioni “, che comporta o l’eccitazione o il cambiamento dell’autostima. Inoltre, i bambini in giovane età non imparano efficacemente. Questo può variare in base a diversi fattori come, perdere facilmente la concentrazione, annoiarsi, sentirsi a disagio o persino ansiosi. Tuttavia, ai bambini piace praticare nuove abilità e tecniche; ecco perché ai bambini piace contare costantemente le cose o gridare i nomi dei numeri con tanta enfasi. Con questo, possiamo concludere che il concetto di pratica è un’abilità importante. Le abilità possono diventare automatiche, liberando uno spazio mentale che aiuta ad imparare cose nuove. Nel processo sociale di apprendimento, “l’imitazione e l’istruzione giocano un ruolo fondamentale”. Questa frase comunica che abbiamo bisogno di fornire esempi e opportunità in cui i bambini imparano attraverso l’osservazione, la riflessione, le istruzioni e le prove. I bambini piccoli normalmente lo fanno automaticamente e si divertono a farlo; individuando similitudini o oggetti che si ripetono (Gifford, 2005).

Per capire l’approccio recreaMATHS, dobbiamo capire cosa piace di più fare ai bambini Ai bambini piccoli piace rappresentare le cose illustrandole e questo coinvolge anche il pensiero spaziale. Riferendosi all’esempio di Gifford: “se i bambini scelgono di rappresentare un tetto con un triangolo, devono avere identificato che entrambe le forme hanno lati spioventi.” La rappresentazione è un processo di apprendimento significativo e per far sì che i bambini inizino a rappresentare le cose, è essenziale che riconoscano alcune caratteristiche chiave. La rappresentazione può essere attiva o visiva, può coinvolgere parole o simboli; non influisce sul processo di apprendimento. L’approccio recreaMATHS incoraggia l’impegno.

Per esempio, indovinare quanti orsacchiotti entrano in una scatola o quale forma tridimensionale può essere nascosta in una scatola ciclica, aiuta a coinvolgere i bambini piccoli e ad assorbire informazioni su forme, dimensioni, mentre si gioca. Indovinare a caso – o altrimenti in un termine matematico – predire, focalizza l’attenzione di un bambino e può coinvolgere la visualizzazione durante il loro processo di pensiero. Trovare la risposta corretta riflette il feedback ai bambini e viene quindi usato come consiglio nei tentativi successivi (Gifford, 2005).

Inoltre, un importante metodo di insegnamento è quello di fornire una serie di esempi, sfidando le idee sbagliate dei bambini in matematica, mostrando un po’ di confusione, modellando gli errori. Questa metodologia può incoraggiare i bambini a fare domande come “E se…?” e “Quanti diversi…?”, che possono aiutarli a testare quali sono i loro limiti di idee e possono prevenire possibili malintesi. Una parte della procedura inventiva è il gioco combinatorio – prendere due cose non correlate e metterle insieme per generare nuove idee – o il gioco associativo – una forma di gioco in cui un gruppo di bambini partecipa ad attività simili – a qualsiasi età e livello.

In questo modo, i bambini possono essere incoraggiati a giocare con concetti matematici distinti fornendo strutture aperte e a sostenere l’esplorazione di potenziali alternativi e nuove connessioni. Gifford suggerisce che la difficoltà di un bambino piccolo con la matematica potrebbe essere dovuta alla mancanza della “consapevolezza del processo esecutivo come il processo di memorizzazione e la procedura di calcolo.(Gifford, 2005).

Molto spesso i bambini hanno quasi una percezione più profonda di quello che stanno vedendo

Fresno State professor Kim Morin.

Alcuni approcci significativi di insegnamento della matematica per gli studenti della scuola materna possono quindi essere riassunti come segue:

• Dimostrazione e istruzioni
• Collegamento ed esplorazione fornendo esempi che ispireranno i bambini a testare le loro idee
• Mentre si discute i bambini possono essere incoraggiati ad usare il linguaggio matematico
• Incoraggiare la rappresentazione e la visualizzazione
• Porre un problema, incoraggiare la previsione attraverso il gioco e dare un feedback
• Incontrare errori e malintesi
• Dimostrare e incoraggiare la riflessione del pensiero

5.1.1 – Apprendimento multisensoriale:

Passiamo all’apprendimento multisensoriale. Quando imparano la matematica, i bambini piccoli usano praticamente tutti i loro sensi: per esempio, i ricercatori hanno scoperto che i bambini piccoli possono rilevare i cambiamenti nei numeri con i suoni e con la visualizzazione. I bambini piccoli possono usare i loro movimenti di tutto il corpo per esprimere o designare le cose. Questo può essere collegato all’idea di “schemi” di azione – si riferisce al concetto fondamentale dello sviluppo intellettuale e alla variabilità delle pratiche e dei linguaggi per rappresentare problemi decisionali consecutivi (Seel, 2012) – o a schemi di comportamento spaziale. I bambini tendono a sviluppare una serie di movimenti, come su e giù, intorno e intorno, che di solito ripetono e che per esempio possono usare nei loro disegni. L’uso di gesti di immagini visive sembra essere principalmente efficace per contare i numeri, che si basa sulla capacità dei bambini di identificare il numero delle cose senza contare. Per esempio affinché i bambini ricordino e riconoscano I numeri come schemi ottici, oggetti come i dadi e il domino possono aiutarli a visualizzare i numeri ed i simboli.

5.1.2 – Incorporare il discorso e il ragionamento matematico attraverso l’esperienza ordinaria del bambino e il gioco iniziato dal bambino. Esperienze centrate sul bambino VS esperienze di gruppo in recreaMATHS:

Come raccomandazione per l’apprendimento della matematica nella scuola materna – prescolare – sono stati suggeriti sia l’istituzione combinata che quella focalizzata. L’istituzione combinata, è collegata ad un metodo “la matematica è ovunque” – che tra le altre cose – include il gioco iniziato dai bambini – un gioco in cui i bambini scelgono cosa e come giocare e con chi giocare (Drew, 2020) – e il gioco guidato dagli adulti – attività e una routine pianificata dall’insegnante (How Play Is Structured in Early Years Settings to Promote Development, n.d.). La pianificazione della matematica è un passo cruciale e significativo. In questo caso, il piano e gli approcci didattici dovrebbero contenere un equilibrio di attività a durante indeterminata e organizzata insieme a un gioco combinato e focalizzato iniziato dal bambino e guidato dall’adulto.

La creazione di un ambiente matematicamente ricco si basa per il supporto su vari esempi, che dipendono da idee sagge basate sulla matematica e risorse multisensoriali come la tecnologia. L’uso quotidiano della matematica per vari scopi distinti può essere rappresentato da questo ambiente matematicamente ricco (Gifford, 2005).

Sembra che un bambino abbia bisogno di tempo per capire e familiarizzare con i concetti matematici – questo include numeri, strumenti di misura o forme – prima di introdurli. Per esempio, prima di capire o anche solo imparare il valore dei numeri, i bambini hanno bisogno di esercitarsi nel conteggio in modo che si sviluppi in un processo automatico. Inoltre, quando i bambini acquisiscono familiarità con un concetto – in questo caso, useremo come esempio le forme di blocchi – attraverso la pratica, i bambini potrebbero usarle per costruire disegni più complessi, sia nella struttura che nel motivo. Quindi, un bambino ha bisogno di sentire di avere diverse opportunità e di essere incoraggiato dagli insegnanti a familiarizzare attraverso la pratica, l’applicazione matematica del problem-solving, come esaminare contando se le matite colorate sono condivise equamente con ogni bambino.

Anche se, utilizzando la frase “La matematica è ovunque” gli insegnanti possono creare e pianificare attività in cui i bambini non si rendono conto che stanno usando la matematica, sembra essere difficile per gli insegnanti o i bambini riconoscere la matematica nelle circostanze quotidiane. La maggior parte dei bambini dell’asilo trova le attività matematiche stimolanti, piacevoli e rilevanti. Quale bambino non si eccita sentendo grandi numeri, o si diverte a identificare gli schemi e ad abbinare le forme? I bambini piccoli provano soddisfazione quando imparano come contare o quando iniziano a riconoscere i numeri. Inoltre, i bambini, quando sono ancora piccoli, trovano divertente esplorare tutte le possibilità distinte e possono anche creare un nuovo metodo o una soluzione unica a un problema senza rendersene conto. Pertanto, la matematica sembra essere rilevante per i bambini piccoli, tutto quello che dobbiamo fare è incoraggiarli a ‘pensare fuori dagli schemi’. Affinché i bambini vedano tutte le prospettive della matematica in contesti diversi, gli insegnanti potrebbero creare idee coinvolgenti incentrate su modi per rendere la matematica più facile da comprendere.

Come menzionato sopra, le attività che sono sia iniziate dai bambini che guidate dagli adulti sono significative nell’apprendimento del processo matematico. Gli approcci didattici non competitivi e meno direttivi sono più efficaci quando si insegna ai bambini piccoli, poiché questo permette ai bambini di impegnarsi più attivamente e di avere il controllo della strategia di insegnamento. Gli insegnanti devono pianificare una serie di metodi interattivi diversi che considerino la maggiore disuguaglianza di influenza tra i bambini dell’asilo e gli insegnanti e pianificare invece attività che proteggano l’autostima dei bambini. Capire come un bambino assorbe la matematica dipende in parte da come l’insegnante assorbe la matematica e l’apprendimento in generale. Il processo di apprendimento varia tra gli individui a causa di diverse ragioni. Ci sono diversi sviluppi critici nel processo di apprendimento della matematica che gli scienziati non comprendono ancora. Per esempio, non si sa ancora come il cervello di un bambino lavori con le immagini non verbali dei numeri o in quali modi questo sia combinato con il conteggio, o come un’idea astratta possa essere sviluppata da questo. Inoltre, come sono collegate le immagini visive di oggetti e forme di un bambino alla comprensione delle sue proprietà? Nessuno scienziato può dare una risposta precisa, ma un’insegnante, d’altra parte, può offrire preziose intuizioni osservando questo processo di apprendimento e pensiero matematico su basi quotidiane.

5.1.3 – Stabilire un approccio olistico; chiedere , ascoltare e controllare :

Gifford, propone che gli insegnanti prendano in considerazione l’importanza dell’apprendimento olistico dei bambini – può essere definito come il modo di fornire supporto a un bambino nel suo insieme, con entrambi i fattori mentali e sociali (emotivo, fisico, sociale e spirituale) considerati (What Is a Holistic Approach? – Principles for Effective Support, n.d.) – che quindi raccomanda di insegnare tenendo conto di tutti i fattori sopra citati (Gifford, 2005). Una delle caratteristiche chiave più importanti dell’apprendimento olistico, è quella di non fare assunzioni come il modo in cui tu come individuo, interpreti una situazione è lo stesso della persona di fronte a te. Affinché un insegnante sia in grado di fornire un apprendimento olistico ci sono tre abilità importanti: chiedere, ascoltare e controllare (What Is a Holistic Approach? – Principles for Effective Support, n.d.). Questo significa rispettare la curiosità di un bambino nel suo modo unico di apprendere, aiutarlo a capire i suoi punti di forza e sia empatizzare e comprendere le sue preoccupazioni. I bambini della scuola materna hanno la capacità di visualizzare le cose, e hanno la capacità di svilupparla ulteriormente. Per esempio, i bambini possono distinguere i numeri senza contare, il che implica che i bambini capiscono che un numero può essere composto in modi differenti.

Inoltre, i bambini possono istantaneamente riconoscere, o subitizzare – un termine ‘inventato’ dal teorico Piaget, e può essere definito come un’abilità di riconoscere immediatamente il numero totale di elementi in un gruppo senza contare (Subitising and Early Number Sense in Early Years Children – Yellow Door, n.d.) – i numeri, sentendo per esempio. È ampiamente noto che la musica aiuta la memoria e alcune azioni ritmiche possono anche aiutare i bambini a contare, implicando l’apprendimento attraverso la musica o la danza. Molti diversi modi di apprendere possono sembrare promettenti, tuttavia, devono essere studiati in profondità. Un esempio è che i bambini rappresentano i concetti matematici, come i numeri, in un modo unico. Ai nostri giorni, i bambini sono più motivati dalle risorse tecnologiche, che includono robot, stampa 3D, e-book, ecc. Non è chiaro per un insegnante come queste risorse possano essere sviluppate in un ambiente educativo. È qui che entra in scena RecreaMATHS. Approcciare la matematica tramite la narrazione di storie ed esperienze incarnate; l’attivazione del corpo fisico e altri mezzi di comunicazione incarnata e orale come un mezzo per consolidare la conoscenza attraverso l’esperienza incarnata e comunicazione orale. La narrazione di storie matematiche recreaMATHS nella scuola materna:

Secondo Balakrishnan (2008), c’è una connessione complessa tra l’immaginazione e le emozioni di un bambino, e quando queste emozioni sono coinvolte con il materiale, allora i bambini di solito fanno uso della loro immaginazione. Quindi, siccome le storie possono essere collegate all’immaginazione di un bambino, hanno la capacità di provocare risposte emotive. Inoltre, si può sostenere che le narrazioni possono essere collegate in modo complesso con il funzionamento della mente. Per esempio, gli esseri umani “pensano, sognano e percepiscono il mondo in termini di storie”. Gli educatori di matematica passano molto tempo a sviluppare l’abilità logica e analitica del bambino, ma non dedicano tempo a sviluppare una delle abilità più potenti che i bambini hanno: l’immaginazione. Una buona storia stimola le emozioni del lettore e gli offre l’opportunità di usare la sua mente in modo sperimentale, di attivare le sue emozioni, di incoraggiarlo ad apprendere e divertirsi allo stesso tempo, e di “aggiungere profondità alle sue giornate”. Osservando i bambini mentre giocano, possiamo esaminare il modo in cui i bambini giocano e adottano personaggi dalle storie che sentono e ricostruiscono scene che catturano la loro immaginazione. Esaminando il mondo in questo modo, i bambini sono in grado di esplorare ma anche di relazionarsi con i vari argomenti e soggetti che il mondo potrebbe presentare loro (Balakrishnan, 2008).

Nell’ultimo decennio, c’è stato un interesse nel ruolo delle storie utilizzate nell’educazione matematica, sia come strumento cognitivo per la comprensione della matematica che come mezzo per la divulgazione della conoscenza. I bambini tendono a capire i concetti matematici più difficili attraverso il contesto di una storia e solo dopo essere stati impegnati in attività che supportano l’idea. Possiamo concludere che le storie giocano un ruolo importante nello stabilire il significato (Balakrishnan, 2008).

Usare la matematica per raccontare storie e usare storie per spiegare la matematica sono due facce della stessa medaglia. Uniscono ciò che non avrebbe mai dovuto essere separato: i modi dello scienziato e dell’artista di svelare le verità sul mondo

Robert Frucht

In modo simile, la ricerca sull’educazione della matematica ha dimostrato che le azioni del bambino influenzano il suo modo di pensare e come i bambini pensano influenza le loro azioni. Perciò, la cognizione incarnata – l’idea in cui le caratteristiche della ‘cognizione umana’ sono modellate non solo dal nostro cervello ma anche da altre parti del nostro corpo – gioca un ruolo significativo nella comunicazione dei concetti e delle idee matematiche, così come nel permettere ai bambini di evolvere e sperimentare le loro idee. Per esempio, i ricordi creati dal movimento possono preparare gli allievi per azioni future e possono essere recuperati e utilizzati per risolvere compiti simili in situazioni diverse che non impegnano più il movimento, ma una trasformazione mentale dei processi motori. Inoltre, i gesti sono stati ritratti per migliorare l’apprendimento aiutando gli studenti a sviluppare idee esistenti con meno carico cognitivo. Considerando che le mani sono comunemente usate per manipolare gli oggetti, i gesti possono offrire ulteriori feedback e segnali visivi simulando come si muove un oggetto se un bambino lo sta tenendo in mano. Ad esempio, i gesti possono permettere il tracciamento degli oggetti nella mente mentre lo ruotano mentalmente, migliorando la visualizzazione spaziale. Inoltre, i gesti possono anche essere coinvolti nella creazione e formazione di nuove idee formulando nuovi modi di pensare attraverso il movimento. In conclusione, l’idea di base del movimento del corpo come parte di un’attività incarnata sta avendo un impatto positivo sulla cognizione permettendo ai bambini di imparare particolari concetti matematici in modo più vantaggioso rispetto all’apprendimento senza movimento (Tran et al., 2017).

Oltre ai gesti e alla cognizione incarnata, ci sono prove sufficienti che aspetti matematici distinti sono incarnati. Uno degli esempi più riconoscibili è quando i bambini usano le dita per contare e questo li aiuta ulteriormente a generare la soluzione di un problema aritmetico. Questo è più comune nei bambini piccoli, che usano le loro dita in combinazione con attività matematiche. Tale conclusione non è imprevedibile, dato che le dita coprono la gamma di numeri a cui i bambini vengono comunemente avvicinati quando contano. L’uso delle dita è una dimostrazione di cognizione incarnata. In questo esempio di bambini che usano le dita mentre contano, la cognizione incarnata è stata identificata come numerosità incarnata. Una combinazione di procedure per livelli più profondi di elaborazione può essere consentita semplicemente usando i sensi della vista e del suono per un livello più profondo di elaborazione per creare un’indicazione di memoria più forte che permette ai bambini di attivare più percorsi per aiutarli a richiamare quel ricordo specifico in seguito. I ricordi creati attraverso il movimento possono essere recuperati e utilizzati nella risoluzione di compiti simili che non coinvolgono più il movimento fisico ma, invece, una trasformazione mentale di quegli specifici sviluppi motori (Tran et al., 2017).

Il movimento permette ai bambini di ridurre la potenza di elaborazione del loro cervello – carico cognitivo – lasciando più risorse per le attività – procedure cognitive – che hanno come risultato il miglioramento delle capacità di risoluzione dei problemi dei bambini. Per esempio, piuttosto che cercare di immaginare come appare un oggetto quando viene ruotato, i bambini possono ridurre questa ansia, preoccupazione, di registrare informazioni lasciando che le loro mani ruotino l’oggetto e osservando ciò che accadrà. Questo può aiutare i bambini a pensare più profondamente alle relazioni spaziali e permette loro di avere una migliore comprensione dei concetti matematici prima del passaggio a un ragionamento spaziale più astratto. Il legame tra i movimenti fisici concreti e astratti completa la naturale propensione dei bambini all’apprendimento. Questo perché la risoluzione dei problemi nel mondo reale – che richiede di muoversi nello spazio e manipolare oggetti reali – è emersa prima che si sviluppassero forme astratte di pensiero come la matematica. Inoltre, il desiderio naturale di posizionare la cognizione con contesti reali si riflette quindi nelle connessioni mente-corpo di diversi concetti matematici come la numerosità incarnata – come menzionato sopra. Unire il corpo nell’esperienza di apprendimento può, di conseguenza, migliorare la comprensione matematica di un bambino attraverso la fornitura di una connessione tra le nozioni astratte e i referenti concreti. Concludendo, l’uso delle dita è, quindi, un esempio notevole nell’illustrare come le caratteristiche fisiche del corpo di un bambino influenzano il modo in cui i bambini elaborano i numeri (Tran et al., 2017).

5.2 – Abilità di problem solving come approccio recreaMATHS

Due tipi di attività chiave che favoriscono l’apprendimento cognitivo sono stati evidenziati dalla ricerca: il problem solving ed il gioco. Questi due tipi di apprendimento cognitivo possono sovrapporsi l’uno all’altro. Le tecniche di problem solving sono usate sotto forma di gioco (mentre si gioca) o possono anche essere usate al contrario: mentre si gioca per usare queste tecniche di risoluzione dei problemi.

Il concetto di problem solving è stato ampiamente considerato come un quadro significativo durante l’apprendimento. Gli insegnanti potrebbero fornire situazioni possibili che aiutano a far nascere la curiosità e la ricerca di soluzioni di un bambino. Come dimostrazione della vera comprensione, rilevano l’applicazione spontanea di un’idea alla nuova situazione. Una tale comprensione della tecnica di risoluzione dei problemi può essere raggiunta attraverso problemi integranti di attività, come puzzle, giochi al computer, o può anche sorgere da cose che i bambini desiderano fare. Il concetto di problem solving incoraggia molti processi cognitivi, come parlare, prevedere, e anche generare connessioni per trovare le soluzioni. Il problem solving ha un ruolo chiave nell’apprendimento della matematica. Adottando abilità di risoluzione dei problemi, i bambini adottano un modo specifico di pensare che li aiuta con quasi tutti i problemi di matematica che incontrano. Gli studenti che tendono ad ottenere punteggi più alti in matematica hanno sviluppato questo modo diverso di pensare; questo “modo di pensare adatto alla risoluzione di problemi”. I ricercatori hanno scoperto che insegnare ai bambini a risolvere i problemi – iniziando a insegnare i problemi di base – potrebbe aiutare a migliorare la salute mentale del bambino. Gli insegnanti possono introdurre un vocabolario di base per risolvere i problemi sotto forma di brevi storie, giocando con i burattini, o anche parlando di situazioni quotidiane che si presentano loro. Inoltre, un altro approccio per la risoluzione dei problemi può essere impostato facendo domande ai bambini. Per esempio, “Come faresti…?” o “Mostrami come potresti…?”. Nell’asilo e nella scuola materna, queste attività di risoluzione dei problemi possono offrire ai bambini l’opportunità di usare abilità precedentemente apprese per risolvere i problemi attuali, mentre gli insegnanti possono insegnare loro alcune nuove strategie di risoluzione dei problemi. Le sopracitate sono solo alcune tecniche di risoluzione dei problemi. Con la pratica, i bambini della scuola materna saranno in grado di identificare i problemi e le sfide, cercare e trovare fatti che li aiuteranno con il problema, pensare a possibili modi da usare per risolvere il problema – come il brainstorming e il pensiero creativo – e infine usare queste idee per verificare se il problema è risolto. Il passo più importante è pensare in modo creativo e avere la capacità di risolvere i problemi.

Tuttavia, il risultato, in altre parole, la risoluzione effettiva del problema, non è la parte importante. Perciò, rinforzate, enfatizzate e sostenete il pensiero creativo di un bambino, parlando di tutti i modi distinti in cui il bambino ha cercato di risolvere il problema emerso, piuttosto che parlare ed enfatizzare il risultato (Gifford, 2005).

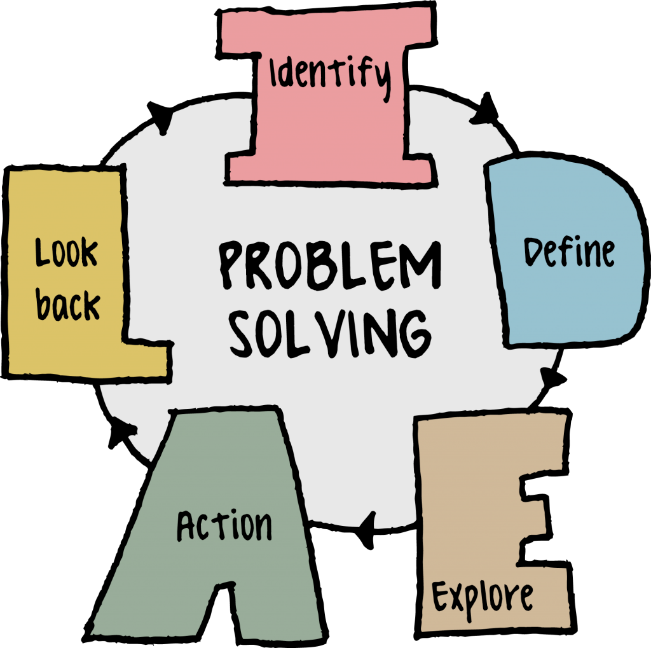
La risoluzione di problemi implica l’uso di approcci di base in modo organizzato per trovare possibili soluzioni ai problemi. Ci sono quattro passi:

1. Definire il problema: identificare la situazione in modo che l’enfasi sia sul problema. (utili tecniche di problem-solving abbracciano l’uso di grafici per aiutare a identificare i passi previsti.
2. Generare soluzioni alternative: ritardare la selezione di una sola soluzione finché non ci sono diverse alternative chiare per la soluzione del problema. Considerare diverse possibilità può migliorare significativamente il valore della soluzione. Per questo passaggio, sia il brainstorming che il lavoro di squadra sono strumenti utili.
3. Valutare e selezionare un’alternativa: considerare e valutare prima di selezionare l’alternativa migliore.
4. Implementare e verificare la soluzione (“KINDERGARTEN PROBLEM SOLVING”, 2019)

Il concetto di problem-solving si presenta in molti aspetti e ambiti diversi. Alcuni problemi possono essere piuttosto minori e sorgere in modo incidentale dalle attività o, dall’altro lato , i problemi possono essere parte di un progetto più grande.

Quindi perché il problem solving è importante??

Secondo Gifford, Piaget (1973) e Vygotsky (1978) che hanno incoraggiato le tecniche di problem solving come un importante “veicolo di apprendimento”. Hanno evidenziato come sia la collaborazione, che la risoluzione guidata dei problemi siano una tecnica significativa. I bambini hanno bisogno di imparare a collegare le abilità che già conoscono a nuove situazioni, per superare le difficoltà attuali e future che incontrano. Quando si risolve un problema, i bambini possono essere incoraggiati a fare nuovi collegamenti con le loro conoscenze attuali e questo può inoltre fornire la motivazione per l’apprendimento. Un vantaggio della tecnica di probem solving è che coinvolge tutti i principali processi cognitivi di apprendimento (attenzione, linguaggio, apprendimento, memoria, percezione e pensiero) nella visualizzazione di soluzioni, nel controllo di possibili errori, e in tutti i contesti di istruzione dati insieme a parlare e riflettere. Il problem solving è importante perché comprende la metacognizione – un pensiero di ordine superiore che abilita il proprio processo cognitivo comprendendolo, analizzandolo e controllandolo (Definizione di metacognizione, n.d.) – usato nella valutazione di strategie e soluzioni (Gifford, 2005).

Le abilità di problem solving possono stimolare un livello superiore di pensiero, compresa un’analisi estesa dei problemi, una sintesi di idee importanti e l’uso della creatività quando si trovano soluzioni non familiari. Inoltre,il problem solving implica di solito un significativo apprendimento emotivo e sociale in cui il successo nel problem solving può migliorare l’autostima del bambino e può aiutarlo a crescere e a sviluppare un “orientamento alla padronanza”. Il problem solving cooperativo può aiutare a formare buone relazioni dando supporto emotivo e cognitivo, che hanno la necessità di abilità sociali. Alcuni esempi di abilità sociali sono: ottenere l’ingresso, sia prendere che dare consigli, e soprattutto risolvere i disaccordi. Per definizione, il problem solving è difficile da perseguire e a volte può minacciare l’autostima di un bambino – o anche di un adulto. Così, l’aiuto e la simpatia di un insegnante giocano un ruolo chiave nel favorire ed incoraggiare un clima favorevole al problem solving in classe. (Gifford, 2005).

Alcune strategie efficaci di problem solving includono:

• Comprendere il problema, guardare il problema nella sua interezza, controllare se i bambini hanno capito il problema facendo loro domande ed analizzandole.
• Preparare, pianificare e prevedere i risultati della soluzione. Per esempio, quando si gioca con i blocchi, raccoglierli tutti insieme prima di iniziare a costruire.
• Monitorare la procedura e il progresso verso l’obiettivo. Per esempio, controllare che tutti i blocchi entrino in una scatola.
• Essere efficienti provando tutte le possibilità -senza ripetere- metodicamente invece di provare a caso. Per esempio, separare le forme di un puzzle in due categorie (o più): quelle che i bambini hanno già provato e quelle non ancora provate.
• Provare diverse opzioni di approccio e valutare strategie distinte. Per esempio, provare le diverse sistemazioni di ogni blocco/forma.
• Migliorare e rifinire una soluzione. Per esempio, risolvendo un puzzle per una seconda volta usando meno mosse ed essendo più veloci.

Tutte le strategie di cui sopra implicano, tra le altre cose, la riflessione e la consapevolezza del processo di pensiero. Gli insegnanti possono consigliare ai bambini di usare le strategie di cui sopra aiutandoli a modellare queste strategie, ma anche incoraggiarli a parlare e confrontare i diversi metodi che hanno usato nella soluzione. Gli insegnanti potrebbero anche raccomandare ai bambini di “preparare” una lista di metodi alternativi tra cui scegliere, trasmettendo una gamma di competenze. Inoltre, i bambini hanno bisogno di acquisire la fiducia di essere flessibili e familiari con il lavoro sulla soluzione di un problema mentre usano tutto ciò che sanno.

Come possono aiutare gli insegnanti? In generale, la nozione di “risoluzione di un problema” è considerata difficile da insegnare. Tuttavia, ai bambini può essere insegnato come usare queste strategie, che di solito coinvolgono idee matematiche. Per esempio, gli insegnanti della scuola materna (o gli adulti in generale), possono insegnare ai bambini a controllare le loro risposte usando il conteggio e possono anche fornire loro le strategie basate su puzzle e giochi al computer. Un esempio che supporta il problem solving è lo scaffolding (un processo attraverso il quale gli insegnanti offrono supporto agli studenti per migliorare l’apprendimento e assisterli nella difficoltà del compito): questo comprende la fornitura di supporto a seconda delle risposte di un bambino, per esempio, suddividendo il problema in passi più piccoli e aiutando i bambini ad attirare l’attenzione sulle caratteristiche chiave. Fare domande è considerata una strategia significativa per aiutare a focalizzare l’attenzione del bambino, ma anche strategie più squisite, come fare commenti o guardare possono essere efficaci. Inoltre, chiedere ai bambini di descrivere (parlare), e di dimostrare i passi di ciò che hanno fatto, può aiutarli a esaminare e valutare il problema. I ricercatori hanno scoperto che quando un insegnante incoraggia i bambini a controllare le loro risposte – i loro passi – significa che in seguito lo farebbero loro stessi. Gifford suggerisce che è utile porre ai bambini più grandi alcune domande ‘auto-organizzative’, di cui i bambini potrebbero servirsi come esempi e su cui basare le loro domande. Un esempio delle diverse fasi di un problema potrebbe essere:

Arrivare al punto:	Cosa stiamo cercando di fare?
Collegarsi all’ esperienza precedente:	Abbiamo mai fatto qualcosa di simile prima?
Pianificare:	Di cosa abbiamo bisogno?
Considerare metodi alternativi:	C’ è un altro modo?
Monitorare i progressi:	Come va fino ad ora?
Valutare le soluzioni:	Funziona?
	Come possimo controllare?
	Possiamo farlo ancora meglio ?

Gli adulti che incoraggiano il comportamento curioso e interrogativo nei bambini suggeriscono che la dimostrazione di atteggiamenti può essere altrettanto importante quanto le strategie di insegnamento. I bambini possono perseguire e diventare fiduciosi nella risoluzione di problemi, con l’aiuto di insegnanti che riconoscono le difficoltà del problem solving ma possono anche stabilire la determinazione che potrebbe aiutarli.

Diversi tipi di problem solving forniscono una varietà di esperienze di apprendimento per i bambini, e possono anche attuare una strategia di insegnamento efficace che valuta e chiarisce tutte le idee sbagliate e aumenta la comprensione dei bambini.

Prospettive di risoluzione dei problemi matematici:

Iniziato dagli adulti: :

• Preparazione – esaminare che ci siano oggetti sufficienti per tutti, per esempio, pennelli, puzzle
• Condividere – esaminare che tutti i bambini abbiano una quantità uguale
• Riordinare – organizzare il magazzino ed esaminare che nulla sia andato perso
• Giardinaggio – sistemare piante e bulbi e prevedere quanto velocemente crescono
• Votare – per storie, canzoni, giochi e in generale votare per le attività
• Pianificare e allestire – un giardino selvaggio o una nuova area di gioco di ruolo
• Comunicazione – piani, misure, inviti con il tempo e le mappe

Iniziata dai bambini::

• Giochi di costruzione e materiali per la creazione di modelli – trovare forme simili, incastrare cose insieme, controllare le dimensioni
• Materiali per creare modelli – generare modelli e stabilire regole, come usare le proprietà delle forme, i movimenti e le posizioni
• Materiali per disegnare e creare immagini – creare forme per rappresentare le cose
• Attività di gioco di ruolo aperte – “qualunque cosa tu voglia che sia il luogo”, per permettere ai bambini di costruire i propri scenari
• Utilità matematiche per bambini da usare durante il gioco – per esempio, calendari fai da te per prendere appuntamenti, calcolatrici per calcolare i prezzi, bilance per pesare un neonato, ecc.

Il libro di George Polya ‘How to solve it, (1945)’, descrive come gli studenti possono adottare abilità di problem solving. Anche se i suoi consigli sono diretti a studenti più grandi (studenti delle scuole superiori e dell’università), possono essere adattati e applicati agli studenti più piccoli della scuola materna. Polya dà quattro passaggi che uno studente dovrebbe seguire quando risolve un problema:

1. Capire il problema; questo primo passo viene regolarmente trascurato perché considerato troppo ovvio dagli studenti. Polya consiglia agli insegnanti di usare alcune delle seguenti domande per aiutare a indirizzare gli studenti nel percorso corretto di comprensione del problema. Alcune domande sono:

• Cosa ti viene chiesto di trovare?
• Puoi definire e descrivere il problema con parole tue?
• Riesci a pensare a un diagramma o a un’immagine che potrebbe aiutarti a comprendere il problema?

Se i bambini non hanno chiaro ciò che deve essere risolto, allora molto probabilmente otterranno la risposta sbagliata. Comprendere il problema è il passo più importante e, in generale, si dovrebbe dare più enfasi a questo passo.

2. Elaborare il piano; Questo è un passo che è in sincronia con la politica di incoraggiare la rappresentazione del pensiero. Questo passo è il piano, o una traduzione del problema sotto forma di un’equazione, un diagramma, un grafico che aiuterà nel processo di risoluzione del problema.
3. Esecuzione del piano; questo è il passo in cui si risolve il piano del passo precedente. Può essere considerato un passo più facile del precedente poiché tutto ciò che deve essere fatto è risolvere l’equazione del passo 2.
4. Guardare indietro (rivedere/estendere); Quando si risolve un problema, è bene guardare indietro e controllare se hai usato tutte le informazioni e controllare che la risposta abbia senso. Fare questo passaggio può aiutare a prevedere una strategia distinta che può essere usata per risolvere problemi futuri.

Comprendere questi quattro passi in giovane età, può dare agli studenti un vantaggio quando risolvono un problema in età più avanzata (Polya, 1945). Per concludere, il problem solving può essere considerato come il fondamento del processo di apprendimento dei bambini. Il problem solving deve essere rispettato, previsto, incoraggiato, e sostenuto nelle classi della scuola materna. Ci sono molteplici opportunità di problem solving che possono verificarsi nella vita quotidiana di un bambino. Nella sezione 5.3 approfondiremo come, utilizzando le esperienze cognitive, sociali, emotive e di movimento del bambino, si faciliti il problem solving e si promuovano approcci utili nel processo di apprendimento duraturo (Britz, 1993).

5.3 – Insegnare ai bambini a vedere e descrivere il loro mondo il modo matematico

Negli ultimi anni, c’è stato un grande progresso nell’insegnamento delle “abilità di pensiero”. La nozione di “abilità di pensiero” è stata identificata come l’introduzione di “ragionamento, indagine e creatività” delle abilità di pensiero. L’indagine combina le capacità di previsione e di pensiero creativo che copre la “ricerca” di varie conclusioni innovative. Gli insegnanti possono usare questo processo incoraggiando i bambini a “pensare ad alta voce”, ma anche a rafforzare e stimolare i metodi che hanno usato per risolvere un problema (Gifford, 2005).

E’ più importante dimostrare la logica della matematica che memorizzare le regole

Alice P. Wakefield

Mentre gli insegnanti di scuola cercano di insegnare ai bambini un’espressione matematica o un problema, di solito forniscono loro la risposta corretta prima che i bambini facciano uno sforzo per pensare quale potrebbe essere la risposta. Tali insegnanti eliminano la necessità della riflessione, che può essere considerata come quella che “sta alla base di un apprendimento duraturo”. Gli insegnanti dovrebbero stabilire tre strategie d’ insegnamento che aiuteranno a rinforzare il pensiero dello studente. Queste tre strategie di insegnamento sono:

‘Incoraggia i tuoi studenti a pensare’. Anche se questo principio non suona irragionevole, la maggior parte degli insegnanti di solito ci passa sopra. Invece di incoraggiare ogni studente a sviluppare il suo modo unico di pensare – il suo senso dei numeri – ci si aspetta che ogni bambino risolva un problema matematico nello stesso modo. Tuttavia, chiedendo semplicemente ai bambini se sono d’accordo con le risposte dei loro compagni o come possono risolvere il problema in modo diverso, l’insegnante li incoraggia a sfidare il loro pensiero.

Passiamo a “incoraggiare i bambini a pensare al pensiero”. Per sostenere l’apprendimento dei bambini nella scuola materna, gli insegnanti dovrebbero incoraggiare i loro studenti a pensare al loro pensiero. In altre parole, aiutarli a formare un concetto di come sono arrivati a quella specifica risposta. Sfidando un bambino della scuola materna a pensare al proprio pensiero, lo si aiuta a diventare più abile e sarà quindi abituato a farlo. Gli insegnanti possono iniziare le loro domande con parole come: “Come”; “Cosa”; “Perché”; “Quale”. Un’idea ancora migliore può essere quella di consigliare loro di lavorare in gruppo. I bambini confronteranno le loro risposte ed eventualmente i diversi metodi utilizzati, ripenseranno le loro soluzioni e potrebbero anche difendere la loro logica.

Infine, “incoraggiare le rappresentazioni del pensiero”. I bambini dovrebbero sapere come rappresentare il loro pensiero con parole, immagini o simboli. Incoraggiare i bambini a riflettere e rappresentare il loro pensiero in classe porterà quindi a pensare ancora di più e a pensare maggiormente al pensiero.

Questi tre principi possono sostenere un’attività mentale più complicata e allo stesso tempo più pratica. Ciononostante, sembra che un approccio che richiede di pensare sia considerato dagli insegnanti un approccio più impegnativo, piuttosto che imparare il libro di testo a memoria. Proprio come un bambino che impara a seguire regole specifiche per arrivare alle risposte corrette non cresce nella comprensione della logica matematica, gli insegnanti che seguono una “ricetta” specifica per raggiungere gli obiettivi matematici non crescono nella comprensione dell’insegnamento e dell’apprendimento (Wakefield, 2001)!

Bambini, adolescenti e adulti, tutti sperimentano in modo unico, trasmettendo una divergenza nei modi in cui impariamo meglio. Il modo in cui un insegnante gestisce i propri studenti può essere influenzato dalla comprensione dei quattro diversi tipi di stili di apprendimento e dall’adattamento all’apprendimento di un individuo. Se lo stile di apprendimento di un individuo non fosse stato attivato, questo individuo potrebbe finire per rimanere indietro rispetto al resto dei suoi compagni di classe. Ci sono quattro diversi stili di apprendimento: gli studenti visivi, gli studenti uditivi, gli studenti di lettura/scrittura e studenti cinestetici. La maggior parte degli studenti di solito rappresenta più di uno stile di apprendimento ciascuno, tuttavia, un insegnante dovrebbe regolare la lezione in modo tale da coprire tutti i diversi stili di apprendimento (Malvik, 2020).

Inoltre, i bambini hanno una preferenza unica nel modo in cui imparano: alcuni sentono, altri fanno, altri vedono, alcuni leggono e altri fanno domande. Tuttavia, tutti i bambini hanno una cosa in comune: tutti imparano meglio quando possono combinare oggetti e argomenti che trovano più interessanti (4 Different Learning Styles You Should Know, n.d.). Pianificare una lezione che soddisfi tutti i sopracitati tipi di studenti può essere considerato più facile quando i bambini sono ancora alla scuola materna. Avendo tutto ciò in mente, gli insegnanti potrebbero usare queste informazioni per insegnare ai bambini come vedere e descrivere il loro mondo in modo matematico. I bambini potrebbero essere incoraggiati a descrivere con parole e linguaggio propri, la matematica che osservano e sperimentano nel mondo reale. La ricerca ha dimostrato che applicando i concetti matematici a situazioni del mondo reale durante il tempo di gioco dei bambini a scuola, li aiuta a stabilire una migliore comprensione dei concetti che stanno imparando. Le raccomandazioni di cui sopra possono essere implementate utilizzando i seguenti passi:

1. Incoraggiare i bambini dell’asilo a rappresentare concetti matematici, soluzioni o processi, usando metodi informali. Questo passaggio può essere completato collegando i concetti matematici alle esperienze dei bambini usando termini e paragoni che sono riconosciuti dai bambini
2. Aiutare i bambini a collegare le loro esperienze e conoscenze informali ai simboli matematici formali, alle procedure e al vocabolario. L’insegnante può iniziare a introdurre alcuni concetti matematici formali, solo dopo che i bambini sembrano essere a loro agio con la rappresentazione informale dei concetti matematici. Gli insegnanti possono procedere collegando insieme le rappresentazioni informali e formali.
3. Usare domande aperte per incoraggiare i bambini ad applicare immediatamente le loro conoscenze matematiche. Le domande che iniziano con “cosa”, “perché”, “come”, stimolano i bambini a pensare al vocabolario e ai concetti matematici informali e formali.
4. Incoraggiare i bambini a identificare la matematica nelle situazioni quotidiane e a parlarne. La conoscenza matematica di un bambino può essere rafforzata dando loro l’opportunità di collegare i concetti matematici appresi in classe al mondo reale (Teaching Math to Young Children, 2013).
5. Per concludere, la matematica è una materia che attrae l’interesse dei bambini solo quando i bambini stessi comprendono che la matematica può essere considerata come uno strumento che può essere utilizzato per risolvere problemi del mondo reale. L’obiettivo dell’approccio recreaMATHS è che gli insegnanti trasferiscano ai bambini della scuola materna questo modo di pensare per risolvere i problemi. Una volta che gli insegnanti capiscono che un basso rendimento internazionale dei bambini in matematica riflette la necessità di una “ricreazione” nell’approccio utilizzato nell’insegnamento dei concetti matematici, allora ci sarà un eccesso nelle abilità matematiche dei bambini. Si consiglia, che l’approccio sarà distinto dall’approccio tradizionale dell’insegnamento e dell’apprendimento della matematica per attirare l’interesse di quanti più bambini possibile (Gifford, 2005). Come menzionato sopra, uno dei modi migliori per gli insegnanti di “matematizzare” i bambini dell’asilo, è quello di utilizzare i concetti matematici nella loro routine quotidiana. Per esempio, sotto forma di giochi o in un modo diverso e divertente per risolvere un problema. Per riassumere, l’atteggiamento conta, quindi, si suggerisce che gli insegnanti incoraggino i bambini a credere nel successo (Pellissier, 2015).

Per concludere, la matematica è una materia che attrae l’interesse dei bambini solo quando i bambini stessi comprendono che la matematica può essere considerata come uno strumento che può essere utilizzato per risolvere problemi del mondo reale. L’obiettivo dell’approccio recreaMATHS è che gli insegnanti trasferiscano ai bambini della scuola materna questo modo di pensare per risolvere i problemi. Una volta che gli insegnanti capiscono che un basso rendimento internazionale dei bambini in matematica riflette la necessità di una “ricreazione” nell’approccio utilizzato nell’insegnamento dei concetti matematici, allora ci sarà un eccesso nelle abilità matematiche dei bambini. Si consiglia, che l’approccio sarà distinto dall’approccio tradizionale dell’insegnamento e dell’apprendimento della matematica per attirare l’interesse di quanti più bambini possibile (Gifford, 2005). Come menzionato sopra, uno dei modi migliori per gli insegnanti di “matematizzare” i bambini dell’asilo, è quello di utilizzare i concetti matematici nella loro routine quotidiana. Per esempio, sotto forma di giochi o in un modo diverso e divertente per risolvere un problema. Per riassumere, l’atteggiamento conta, quindi, si suggerisce che gli insegnanti incoraggino i bambini a credere nel successo (Pellissier, 2015).

La matematica è il linguaggio della logica

Dr. Jie-Qi Chen

116 References:

4 Different Learning Styles You Should Know: The VARK Model. (n.d.). Retrieved October 29, 2020, from https://educationonline.ku.edu/community/4-different-learning-styles-to-know 

Abba, G. (1995). Ruolo del materiale didattico nel processo di apprendimento e integrazione del non vedente in età evolutiva. Tiflologia per l’integrazione, 5 (3), supplem., 34-36. 

Anthony, G., & Walshaw, M. (n.d.). Effective pedagogy in mathematics. 32.

Asha K., Jitendra K. H., Beck M., “L’uso degli schemi visivi per la risoluzione dei problemi matematici, in Difficoltà di apprendimento”, Vol. 8, n. 1, Lehigh University, Bethlehem, 2002. 

Balakrishnan, C. (2008). TEACHING SECONDARY SCHOOL MATHEMATICS THROUGH STORYTELLING. 306. 

Bavelier D, Tomann A, Hutton C, Mitchell T, Corina D, Liu G, et al. (2000) Visual attention to the periphery is enhanced in congenitally deaf individuals. Journal of Neuroscience 20:1–6. 

Best Digital Book in Maths/Sciences 2018 https://innotechtoday.com/digital-book-world-2018/

Britz, J. (1993) Problem Solving in Early Childhood Classrooms. https://files.eric.ed.gov/fulltext/ED355040.pdf 

Candiotta Giusla mateeppina, “la matematica per i sordi”, relatore Enrico Dolza. – Tesi dattiloscritta. – Torino: Università degli studi, 2015-2016. 

Chiara Nanni , Enrica Partesana and Daniela Rocca “Early Identification and Strengthening of Learning Difficulties A Project of Collaboration between School and Neuropsychiatry Service”, Edizione Erickson, DIS Vol. 1, Issue 1, January 2020 

Culture and the arts. (2019). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Wikipedia:Contents/Culture_and_the_arts&oldid=926544104

D. Fabbretti, E. Tomasuolo, “Scrittura e sordità” Carrocci, Roma, 2006 

d’Entremont, Y. (2015). Linking Mathematics, Culture and Community. Procedia – Social and Behavioral Sciences, 174, 2818–2824. https://doi.org/10.1016/j.sbspro.2015.01.973

Davide Antognazza and Silvia Sbaragli “The Influence of the Teacher’s Attitude over the Students’ Commitment Mathematics Education Case “, Edizione Erickson, DIS Vol. 1, Issue 1, January 2020 

Definition of metacognition. (n.d.). Www.Dictionary.Com. Retrieved October 26, 2020, from https://www.dictionary.com/browse/metacognition 

Dooley, T., Dunphy, E., Shiel, G., Butler, W. D., Corcoran, D., Farrell, T., NicMhuirí, S., O’Connor, M., & Travers, J. (n.d.). Mathematics in Early Childhood and Primary Education (3-8 years). 164.

Drew, C. (2020). The 5 Key Features of Child Initiated Play (2020). Helpful Professor. https://helpfulprofessor.com/child-initiated-play/ 

European Math Museums Questionnaire

Fermat Science: https://www.fermat-science.com/

Finkel, D. (2015, June 13). 5 principles of extraordinary math teaching. Math for Love. https://mathforlove.com/2015/06/5-principles-of-extraordinary-math-teaching/ 

Finkel, D. (2016, May 11). Hate Math? Make It Fun With Picture Books, Board Games and More. Math for Love. https://mathforlove.com/press/hate-math-make-it-fun-with-picture-books-board-games-and-more/

Francesco Sella, Daniela Lucangeli and Marco Zorzi “The Mastering of the Cardinality Principle in a Sample of Italian Preschool Children” Edizione Erickson, DIS Vol. 1, Issue 2, May 2020 

Frye, D., Baroody, A., Burchinal, M., Carver, S., Jordan, N., & McDowell, J. (2013). Teaching Math to Young Children. The Institute of Education Sciences (IES), 1–152. https://ies.ed.gov/ncee/wwc/Docs/PracticeGuide/early_math_pg_111313.pdf 

Gifford, S. (2005). Teaching Mathematics 3-5: Developing Learning in the Foundation Stage. http://eds.a.ebscohost.com/eds/ebookviewer/ebook/bmxlYmtfXzIzMzkzM19fQU41?sid=f1519a5c-1edb-4669-8a83-c8f4a4142877@sdc-v-sessmgr01&vid=0&format=EB&rid=1 

Ginsburg, H. P., Inoue, N. & Seo, K. H. (1999). Young children doing mathematics: Observations of everyday activities. In J. Copely (Ed.), Mathematics in the early years (pp.88–99). Reston,VA: NCTM  

Giulia Franconi and Cesare Cornoldi, “A Study on the Change of the Relationship between Mathematics and Metacognition in Different School Levels” Edizione Erickson, DIS Vol. 1, Issue 1, January 2020 

How play is structured in early years settings to promote development. (n.d.). 6. 

How to teach kindergarten and preschool math. (2019, June 24). Kindergarten Lessons. https://www.kindergarten-lessons.com/kindergarten-and-preschool-math/

Instructional Research Group. (2008, January). Mathematics Instruction for Students with Learning Disabilities or Difficulty Learning Mathematics: A Guide for Teachers. Center on Instruction. https://www.researchgate.net/publication/234623037_Mathematics_Instruction_for_Students_with_Learning_Disabilities_or_Difficulty_Learning_Mathematics_A_Guide_for_Teachers 

Jayanthi, Madhavi & Gersten, Russell & Baker, Scott. (2008). Mathematics Instruction for Students with Learning Disabilities or Difficulty Learning Mathematics: A Guide for Teachers. Center on Instruction.

Johansson, M. (2015). Perceptions of mathematics in preschool “-now we have a way of talking about the mathematics that we can work with.”

Jones, C. (2009). Interdisciplinary Approach: Advantages, Disadvantages, and the Future Benefits of Interdisciplinary Studies. 

Khasnabis, C., Motsch, K. H., Achu, K., Jubah, K. A., Brodtkorb, S., Chervin, P., Coleridge, P., Davies, M., Deepak, S., Eklindh, K., Goerdt, A., Greer, C., Heinicke-Motsch, K., Hooper, D., Ilagan, V. B., Jessup, N., Khasnabis, C., Mulligan, D., Murray, B., … Lander, T. (2010). Non-formal education. In Community-Based Rehabilitation: CBR Guidelines. World Health Organization. https://www.ncbi.nlm.nih.gov/books/NBK310920/

KINDERGARTEN PROBLEM SOLVING. (2019, February 27). Kindergarten Lessons. https://www.kindergarten-lessons.com/kindergarten_problem_solving/ 

L’ Europe mathématique/Mathematical Europe: Histoires, mythes, identités publié par Catherine Goldstein, Jeremy Gray, Jim Ritter

Le Point Hors-Série, La Méthode Singapour, December 2017

Les Défis de l’enseignement des mathématiques dans l’éducation de base, Michèle Artigue, Unesco report, 2011

Making the Connection between Culture and Mathematics Northwestern University | School of Education & Social Policy. (n.d.). Retrieved December 18, 2020, from https://www.sesp.northwestern.edu/news-center/inquiry/2009-spring/making-the-connection.html

Malvik, C. (2020). 4 Types of Learning Styles: How to Accommodate a Diverse Group of Students. https://www.rasmussen.edu/degrees/education/blog/types-of-learning-styles/ 

Maria Grazia Palermo, “Matematica e scienze con l’alunno sordo : teaching mathematics and science of to the deaf students”; relatore Enrico Dolza. – Tesi dattiloscritta. – Torino : Università degli studi, 2015 (TESI 136). 

Mathematics in Early Childhood and Primary Education (3-8 years), NCCA,

Mathematikum museum: https://www.mathematikum.de/

Mmaca museum: https://mmaca.cat/

Mok, O. N. A. (2011). Non-formal learning: Clarification of the concept and its application in music learning. Australian Journal of Music Education, 1, 11–15.

Navet museum: https://www.navet.com/

Neculae Dinuță – Methodical aspects regarding the interdisciplinary approach of mathematical contents in preschool education. Procedia – Social and Behavioral Sciences 180 ( 2015 ) 780 – 787 

NMC HorizonReport: 2017 Higher Education Edition

Non-formal education. (1999). https://assembly.coe.int/nw/xml/XRef/X2H-Xref-ViewHTML.asp?FileID=8807&lang=EN

Non-formal education. (2020, June 22). http://uis.unesco.org/en/glossary-term/non-formal-education

Observation Cooperation Information Museums: https://ocim.fr/2020/12/approches-sociales-et-inclusives-des-musees-et-des-lieux-de-culture-scientifique/

Oldridge, M. (2019). The Playful Approach to Math. Edutopia. https://www.edutopia.org/article/playful-approach-math

Papadakis, S., Kalogiannakis, M., & Zaranis, N. (2016). Improving Mathematics Teaching in Kindergarten with Realistic Mathematical Education. Early Childhood Education Journal, 45(3), 369–378.

Pellissier, H. (2015). Why early math is just as important as early reading. Parenting. https://www.greatschools.org/gk/articles/early-math-equals-future-success/ 

Pigliacampo R.,” Lingua e Linguaggio nel sordo, analisi e problemi di una lingua visivo-manuale”, Armando Editore, Roma, 1998. 

Pourquoi l’école a-t-elle enseigné le comptage-numérotage pendant près de 30 années ?, Rémi Brissiaud, september 2014

Press article on maths museums: https://lepetitjournal.com/francfort/a-voir-a-faire/mathematikum-le-premier-musee-interactif-des-mathematiques-giessen-attire-les-visiteurs-77890

Rosy Luca, “Insegnare matematica ad allievi con disabilità acustica = teaching mathematics for deaf student”, rel. Cecilia Maria Marchisio. – Tesi dattiloscritta. – Torino : Università degli Studi, PAS Piemonte – a.a. 2013-2014 (TESI 119). 

Samarapungavan, Patrick, Mantzicopoulos, A. H. P. (2011). What Kindergarten Students Learn in Inquiry-Based Science Classrooms. Taylor & Francis Group, 416–470. https://doi.org/10.1080/07370008.2011.608027 

Seel, N. M. (2012). Action Schemas. In N. M. Seel (Ed.), Encyclopedia of the Sciences of Learning (pp. 73–75). Springer US. https://doi.org/10.1007/978-1-4419-1428-6_356 

Sensorineural Hearing Loss Occurs in the Cochlea | MED-EL, https://www.youtube.com/watch?v=EfzvT_WR0x4. 

Simonetta Maragna, “ Una scuola oltre le parole : educare il bambino sordo alla lingua parlata e scritta : con esempi di unità didattica” ; presentazione di Virginia Volterra. – Milano : F. Angeli, 2003 (Cap. 4: Le unità didattiche. Area Logico-matematica). 

Soares, N., Evans, T., & Patel, D. R. (2018). Specific learning disability in mathematics: a comprehensive review. Translational Pediatrics, 7(1), 48–62. https://doi.org/10.21037/tp.2017.08.03 

Spiteri, M. (2016, August 18). The benefits of non-formal learning [Text]. EPALE – European Commission. https://epale.ec.europa.eu/en/blog/benefits-non-formal-learning

St Patrick’s College, Charles Sturt University, & Educational Research Center. (2014a). Mathematics in Early Childhood and Primary Education (3–8 years) Definitions, Theories, Development and Progression (No. 17). National Council for Curriculum and Assessment. 

St Patrick’s College, Charles Sturt University, & Educational Research Center. (2014b). Mathematics in Early Childhood and Primary Education (3–8 years) Teaching and Learning (No. 18). National Council for Curriculum and Assessment. 

Subitising and Early Number Sense in Early Years Children—Yellow Door. (n.d.). Retrieved October 27, 2020, from https://www.yellow-door.net/blog/what-is-subitising/ 

Teaching Math to Young Children. (2013). 165. 

Teresa Ferraiuolo and Rosanna Coseglia, ”Playing with Numbers and Letters An Enhancement Experience in an Inclusive Context” Edizione Erickson, DIS Vol. 1, Issue 1, January 2020 

Terezinha Nunes, “Teaching mathematics to deaf children” – London and Philadelphia: Whurr, 2004. 

Tiziana Raso, “Metodologie didattiche per l’insegnamento della matematica ai sordi : didactic methods for teaching mathematics to deaf students”; relatore Enrico Dolza. – Tesi dattiloscritta. – Torino : Università degli studi, 2015. (TESI 138). 

Tran, C., Smith, B., & Buschkuehl, M. (2017). Support of mathematical thinking through embodied cognition: Nondigital and digital approaches. Cognitive Research: Principles and Implications, 2(1), 16. https://doi.org/10.1186/s41235-017-0053-8 

Tudge, J., & Doucet, F. (2004). Early mathematical experiences: Observing young black and white children’s everyday activities. Early Childhood Research Quarterly, 19(1), 21–39. 

UDL: The UDL Guidelines. (2021, April 9). The UDL Guidelines. https://udlguidelines.cast.org. 

Una app dedicata ai bambini ciechi per imparare la matematica : https://www.superabile.it/cs/superabile/istruzione/una-app-dedicata-ai-bambini-ciechi-per-imparare-la-matematica.html. 

Understanding teaching professionals’ digital competence: What do PIAAC and TALIS reveal about technology-related skills, attitudes, and knowledge?, R. Hamalainen et al., 2020

Valentina Franceschina “Il bambino non vedente e la matematica: quali strumenti è opportuno utilizzare per facilitare questo apprendimento?” tesi di laurea in scienze della educazione. 

Valentina Mengoni and Laura Maria Castagna, “Comparison between Reading Performances of Children with Specific Learning Disabilities and Learning Difficulties by Using Times New Roman and EasyReading Writing Font” Edizione Erickson, DIS Vol. 1, Issue 2, May 2020 

Vodopivec, J. (in press). COOPERATIVE LEARNING AND SUPPORT STRATEGIES IN THE KINDERGARTEN. Metodički Obzori. 

Vygotsky L. S., “Pensiero e linguaggio”, a cura di Costa A., Giunti, Firenze, 1966.Ø  M. C. Caselli, S. Maragna, V. Volterra, “Linguaggio e sordità”, il Mulino, 2006 

Wakefield, A. P. (2001). It’s more importantto demonstratethe logic of math than to memorize rules. 5. 

What are strategies for teaching a student with a math-related learning disability? | DO-IT. (n.d.). What Are Strategies for Teaching a Student with a Math-Related Learning Disability? Retrieved January 12, 2021, from https://www.washington.edu/doit/what-are-strategies-teaching-student-math-related-learning-disability 

What are typical challenges students with math-related learning disabilities face? | DO-IT. (n.d.). What Are Typical Challenges Students with Math-Related Learning Disabilities Face? Retrieved January 14, 2021, from https://www.washington.edu/doit/what-are-typical-challenges-students-math-related-learning-disabilities-face?323= 

What is a holistic approach? – Principles for effective support. (n.d.). Retrieved October 27, 2020, from https://www.health.nsw.gov.au/mentalhealth/psychosocial/principles/Pages/holistic.aspx 

What Is Culture? Definition, Meaning and Examples | Live Science. (n.d.). Retrieved November 13, 2020, from https://www.livescience.com/21478-what-is-culture-definition-of-culture.html

What is non formal education and why it is important. (2018, September 18). Dothegap / Sube Tu Experiencia. Descubre Otras Afines. Conecta. https://dothegap.com/blog/en/what-is-non-formal-education-and-why-it-is-important/

What is non-formal education? (2015). https://infed.org/mobi/what-is-non-formal-education/

What’s Dyscalculia? (n.d.). What’s Dyscalculia? Retrieved January 15, 2021, from https://www.dyscalculia.org/dyscalculia/what-s-dyscalculia 

Yeo, D. (2003). Dyslexia, Dyspraxia and Mathematics (1st ed.). Wiley. 

Zisopoulou, E. (2019). Collaborative learning in kindergarten: Challenge or reality? Erken Çocukluk Çalışmaları Dergisi, 3(2), 335–351. https://doi.org/10.24130/eccd-jecs.1967201932113