5.1 – Understanding the recreaMATHS approach
So, what is a ‘recreaMATHS approach’? How can we recreate the approach in learning mathematics in kindergarten?
In this chapter, we will give answers to the above questions and try to explain to you in more depth about the recreaMATHS approach. Part of the recreaMATHS approach is based on the wider mathematical competence in kindergarten. By considering how a child learns in general, we can determine a way on how to teach mathematics to kindergarten children. Teachers can identify teaching approaches that avoid overpressure and negative attitudes towards the learning process of a child. Learning is a complicated development, where each individual child learns in a distinct way and evolves this learning at their own pace. There are many aspects involved in this process, however, all children share a developing brain and body, and can be greatly influenced by their experiences – both social and cultural – which can help in the learning process (Gifford, 2005).
Learning can be considered as an ‘emotionally charged business’, which either involves excitement or change to self-esteem. Additionally, children of a young age, do not learn effectively. This can vary on different factors such as, losing their concentration easily, become bored, uncomfortable, or even anxious. Nonetheless, children enjoy practicing new skills and techniques; that is why children like to constantly count things or shout out numerals’ names with such emphasis. With this, we can conclude that the concept of practicing is an important skill. Skills can become automatic, setting free some mental space that helps in learning new things. In the social process of learning, ‘imitation and instruction play a leading role’. This sentence conveys that we need to provide examples and opportunities where children learn through observation, reflection, instructions, and rehearsal. Young children normally do this automatically and enjoy doing it; spotting similarities or objects repeating themselves (Gifford, 2005).
To understand the recreaMATHS approach, we need to understand what children enjoy doing best. Young children enjoy representing things by illustrating them and this also involves thinking spatially. Referring to Gifford’s example: ‘if children choose to represent a roof by a triangle, they must have identified that both shapes have sloping sides.’ Representation is a significant learning process and in order for children to start representing things, it is essential for them to recognize some key features. Representation can be active or visual, it can either involve words or symbols; it does not affect the process of learning. The recreaMATHS approach encourages engagement.
For example, guessing how many teddy bears fit in a box or what 3-dimensional shape can be hidden in a cyclical box, helps engage young children and absorb information about shapes, sizes, while playing. Random guessing – or otherwise in a mathematical term – predicting, focuses the attention of a child and can involve visualization during their thinking process. Finding out the correct answer reflects feedback to the children and is therefore used as advice in the following attempts (Gifford, 2005).
Moreover, an important teaching method is by providing a range of examples, challenging children’s’ mathematical misconceptions, displaying some confusion, modeling errors. This methodology may encourage children to ask questions such as ‘What if…?’ and ‘How many different…?’, which may help them test what their boundaries of ideas are and may prevent possible misconceptions. A part of the inventive procedure is the combinatorial play – taking two unrelated things and putting them together to generate new ideas – or associative play – a form of play in which a group of children participate in similar activities – at any age and level.
Thus, children may be encouraged to play with distinct mathematical concepts by providing open-ended frameworks and to support the exploring of alternative potentials and new connections. Gifford suggests that a young child’s difficultness with mathematics might be due to the lack of the ‘awareness of executive process’ such as the process of memorization and the calculation procedure (Gifford, 2005).
Very often young children have an almost deeper perception of what they’re seeing
Fresno State professor Kim Morin.
Some significant mathematical teaching approaches for kindergarten students may therefore be summarized as follows:
- Demonstration and instructions
- Connecting and exploring by providing examples which will inspire children to test their ideas
- While discussing children may be encouraged to use mathematical language
- Encouraging representation and visualization
- Posing a problem, encouraging prediction through play, and giving feedback
- Encountering errors and misconceptions
- Demonstrating and encouraging the reflection of thinking
5.1.1 – Multisensory Learning:
Moving on to multisensory learning. When learning mathematics, young children use mostly all their senses: for example, researchers have found that young children can detect the changes in numbers with sounds and by visualization. Young children may use their whole-body movements to express or designate things. This can relate to the idea of action ‘schemas’ – refers to the fundamental concept of intellectual development and to the variability of practices and languages for representing consecutive decision-making problems (Seel, 2012) – or spatial appears to be principally effective for counting numbers, that builds on children’s capability to identify the number of things without counting. For example, for children to remember and recognize numbers as optical patterns, objects such as dice and dominoes may help them visualize numbers and symbols.
5.1.2 – Embedding mathematical discourse and reasoning through a child’s ordinary experience and child’s-initiated play. Child-centred VS Group experiences in recreaMATHS:
As a recommendation for the learning of mathematics in kindergarten – preschool – both combined and focused establishment have been suggested. Combined provision, is connected with a ‘math is everywhere’ method – which among other things – includes child-initiated play – a play where children choose what and how to play and who to play with (Drew, 2020) – and adult-led play – activities and a routine planned by the teacher (How Play Is Structured in Early Years Settings to Promote Development, n.d.). The planning of mathematics is a crucial and significant step. In this case, the plan and the teaching approaches should contain an equilibrium of open-ended and organized activities along with a combined and focused child-initiated and adult-led play.
Creating a mathematically rich environment relies for support on various examples, which depend on wise ideas based on mathematics and multisensory resources such as technology. The everyday use of mathematics for various distinct purposes can be depicted by this mathematically rich environment (Gifford, 2005).
It appears that a child needs time to understand and become familiar with the mathematical concepts – this includes numbers, measuring tools, or shapes – before introducing it to them. For example, before understanding or even learning about the value of numbers, children need to practice their counting so that it develops into an automatic process. Furthermore, when children become familiar with a concept – in this case, we will use as an example shapes of blocks – through practice, children could use them to build more complex designs, in both structure and pattern. Hence, a child needs to feel that they have several opportunities and are encouraged by the teachers to familiarise through practice, the mathematical application of problem-solving, such as examining by counting if the colour pencils are shared equally to each child.
Even though, by using the phrase ‘Mathematics is Everywhere’ teachers can create and plan activities in which children do not realize they are using mathematics, it seems to be difficult for the teachers or the children to recognize the mathematics in everyday circumstances stimulating, pleasant, and relevant. What child does not get excited by hearing large numbers, or enjoy identifying patterns, and matching the shapes? Young children feel satisfaction when they learn how to count or when they begin recognizing numbers. Moreover, children, when still young, find it enjoyable to explore all distinct possibilities and may even create a new method or unique solution to a problem without realizing it. Therefore, mathematics seems to be relevant to young children, all we need to do is encourage them to ‘think out of the box’. In order for children to see all the prospects for mathematics in distinct contexts, teachers could create engaging ideas focused on ways of making math easier to comprehend.
As mentioned above, activities which are both child-initiated and adult-led are significant in the learning of the mathematical process. Non-competitive and less directive teaching approaches are more effective when teaching young children, since, this allows children to engage more actively and be in control of the teaching strategy. Teachers need to plan a range of distinct interactive methods that consider the greater inequity of influence between kindergarten children and teachers and instead plan activities that protect children’s self-esteem. To understand how a child absorbs mathematics partially depends on how the teacher absorbs mathematics and learning in general. The learning process varies between individuals due to several different reasons. There are several critical developments in the learning process of mathematics which scientists do not understand yet. For example, it is not yet known how a child’s brain works with the non-verbal images of numbers or in which ways this is combined with counting, or how an abstract idea can be developed by this. Additionally, how are a child’s visual images of objects and shapes related to this child’s understanding of its properties? No scientist can give an accurate answer, but a teacher, on the other hand, can offer valuable insights by observing this process of learning and thinking mathematically on an everyday basis.
5.1.3 – Establishing a holistic approach; asking, listening and checking:
Gifford, suggests that teachers should take into account, the importance of children learning holistically – can be defined as the way of providing support to a child as a whole, with both mental and social factors (emotional, physical, social as well as spiritual wellbeing) considered (What Is a Holistic Approach? – Principles for Effective Support, n.d.) – which therefore recommends teaching while taking into account all aforementioned factors (Gifford, 2005). One of the most important key features of learning holistically, is to make no assumptions such as how you as an individual, interpret a situation is the same as the person opposite you. For a teacher to be able to provide holistic learning there are three important skills: asking, listening, and checking (What Is a Holistic Approach? – Principles for Effective Support, n.d.). This means respecting a child’s curiosity in their unique way of learning, helping them figure out their strengths and both empathize and sympathize with their concerns. Kindergarten children have the ability to visualize things, and have the capability to develop this even further. For instance, children can distinguish numbers without counting which implies that children understand that a number could be made-up in distinct ways. In addition, children can instantaneously recognize, or subitize – a term ‘invented’ by Piaget, a theorist, and can be defined as a skill to immediately recognize the total number of items in a group without counting (Subitising and Early Number Sense in Early Years Children – Yellow Door, n.d.) – numbers, by hearing for example. It is broadly known that music helps the memory and some rhythmical actions may even help children count, implying learning through music or dance. Several different ways of learning may seem promising, nonetheless, they need to be studied in depth. One example is that children represent mathematical concepts, such as numbers, in a unique way. In our days, children are most motivated by technological resources, which include robots, 3D print, e-books, etc. It is unclear for a teacher how these resources could be developed in an educational setting. This is where recreaMATHS steps in.
Approaching mathematics through story-telling and embodied experiences; the activation of the physical body and other means of embodied and oral communication as a means of consolidating knowledge through experience embodied and oral communication. The recreaMATHS mathematical story-telling in kindergarten:
According to Balakrishnan (2008), there is a complicated connection between the imagination and emotions of a child, and when these emotions are involved with the material, then children usually make use of their imagination. Therefore, since stories can be linked to a child’s imagination, they have the ability to provoke emotional responses. Additionally, one can argue that narratives can be connected in a complex way with how the mind works. For instance, human beings “think, dream, and perceive the world in terms of stories”. Mathematics educators spend a lot of time in developing a child’s logical and analytical ability but spend no time in developing one of the most powerful abilities the children have – imagination. A good story stirs the reader’s emotions and offers them the opportunity to use their mind in an experimental way, to activate their emotions, encourage them to learn and enjoy at the same time, and to “add depth to their days”. By observing children while playing, we can examine the way children play and adopt characters from the stories they hear and rebuild scenes that capture their imaginations. By examining the world in such a way, children are able to explore as well as relate to several topics and subjects the world might throw at them (Balakrishnan, 2008).
In the past decade, there has been an interest in the role of stories used in mathematical education, both as a cognitive tool for the understanding of mathematics and as a means of knowledge dissemination. Children tend to understand the more difficult math concepts through the context of a story and only after they are engaged in activities that support the idea. We can conclude that stories play an important role in the establishment of meaning (Balakrishnan, 2008).
Using mathematics to tell stories and using stories to explain mathematics are two sides of the same coin. They join what never should have been separated: the scientist’s and the artist’s ways of uncovering truths about the world
Robert Frucht
Similarly, research on the education of mathematics has shown that the child’s actions influence how they think and how children think influences their actions. Therefore, embodied cognition – the idea in which the features of ‘human cognition’ are shaped not only by our brains but also by other parts of our body – plays a significant role in communicating the mathematical concepts and ideas, as well as in allowing children to evolve and experiment their ideas. For example, memories created by movement can prepare learners for future action and can be retrieved and used in solving similar tasks in different situations that no longer engage movement, but instead a mental transformation of the motor processes. Furthermore, gestures have been portrayed to improve learning by helping learners develop existing ideas with less cognitive load. Considering that hands are commonly used to manipulate objects, gestures may offer additional feedback and visual signals by simulating how an object moves if a child is holding it. For instance, gestures may allow the tracking of objects in the mind while mentally rotating it, improving spatial visualization. Moreover, gestures can be also involved in the creation and shaping of new ideas by formulating new ways of thinking through movement. In conclusion, the basic idea of body movement as part of an embodied activity is having a positive impact on cognition by allowing children to learn particular mathematical concepts more advantageously than learning them without movement (Tran et al., 2017).
In addition to gestures and embodied cognition there is sufficient evidence that distinct mathematical aspects are embodied. One of the most recognizable examples is when children use their fingers to count and this helps them further in generating the solution to an arithmetic problem. This is most common in young children, which use their fingers in combination with mathematical tasks. Such a conclusion is not unpredictable given the fact that fingers cover the number range within which children are commonly introduced to when counting. The usage of fingers is a demonstration of embodied cognition. In this example, of children using their finger while counting, embodied cognition has been identified as embodied numerosity. A combination of procedures for deeper levels of processing can be allowed by simply using the senses of sight and sound for a deeper level of processing to create a stronger memory indication that allows children to activate multiple paths in helping them recall that specific memory later on. Memories created through movement can be retrieved and used in solving similar tasks that no longer involve physical movement but instead, a mental transformation of that specific motor developments (Tran et al., 2017).
Movement allows children to bring down their brain’s processing power – cognitive load – leaving more resources for the activities – cognitive procedures – which result in the improvement of children’s problem-solving abilities. For instance, rather than trying to imagine how an object appears when rotated, the children may reduce this anxiety, concern, of recording information by letting their hands rotate the object and observing what will happen. This can help children in thinking more deeply about the spatial relations and allows them to have a better understanding of math concepts before the transition to a more abstract spatial reasoning. The link between the concrete and abstract physical movements complements children’s natural propensity for learning. This is because problem-solving in the real world – required moving through space and manipulating actual objects – emerged before the abstract forms of thought such as mathematics developed. Furthermore, the natural desire to position cognition with real contexts is therefore reflected in the mind-body connections of several mathematical concepts such as embodied numerosity – as mentioned above. By combining the body into the learning experience can, consequently, improve a child’s mathematical understanding through the provision of a connection between the abstract notions and the concrete referents. Concluding, the use of fingers is, therefore, a remarkable example in illustrating how a child’s physical body features influence the way children process numbers (Tran et al., 2017).
5.2 – Problem-Solving Skills as a recreaMATHS approach
Two key types of activity which foster cognitive learning, have been highlighted by research: problem-solving and play. These two cognitive learning types can overlap with one another. Problem-solving techniques are used in the form of a game (while playing) or can even be used in the other way round: while playing to use these problem-solving techniques. The concept of problem-solving has been broadly considered as a significant framework while learning. Teachers could provide possible situations that help arise the curiosity and solution-seeking of a child. As a demonstration of the true understanding, detect the spontaneous application of an idea to the new situation. Such an understanding of the problem-solving technique can be achieved through problems integral to activities, such as puzzles, games on the computer, or can even rise out of things children wish to do. The concept of problem-solving, encourage many cognitive processes, such as talking, predicting, and even generating connections to find the solutions.
Problem-solving has a key role in learning mathematics. By adopting problem-solving skills, children adopt a specific way of thinking which helps them with almost every math problem they come across. The students that tend to achieve higher scores in math have developed this different way of thinking; this ‘problem-solving way’ of thinking. Researchers have found that teaching children problem-solving skills – by beginning to teach basic problems – might help improve a child’s mental health. Teachers can introduce some basic vocabulary of solving problems in the form of short stories, playing with puppets, or even talk about everyday situations that occur to them. Furthermore, one more approach for problem-solving can be set by asking the children questions. For example, “How would you…?” or “Show me how you could…?”. In kindergarten and preschool, these problem-solving activities, may offer to children the opportunity to use previously learned skills to solve current problems while teachers can teach them some new problem-solving strategies. The aforementioned are only a few problem-solving techniques. Through practicing, kindergarten children will be able to identify the problems and challenges, search and find facts that will help them with the problem, think of possible ways to use in solving the problem – such as brainstorming and creative thinking – and lastly use these ideas to test if the problem is solved. The most important step is thinking creatively and having the ability to solve problems.
Nonetheless, the result, in other words, actually solving the problem, is not the important part. Therefore, reinforce, emphasize and support a child’s creative thinking, while talking about all the distinct ways the child tried to solve the emerged problem rather than talking and emphasizing the outcome (Gifford, 2005).
Problem-solving involves using basic approaches in an arranged way to find possible solutions to problems. There are four steps:
- Define the problem: identify the situation so that the emphasis is on the problem. (helpful problem-solving techniques embrace using charts to help identify the expected steps.
- Generate alternative solutions: delay the selection of just one solution until there are several clear problem-solving alternatives. Considering several possibilities can significantly improve the value of the solution. For this step, both brainstorming and teamwork are beneficial tools.
- Evaluate and select an alternative: consider and evaluate before selecting the best alternative.
- Implement and follow up on the solution (“KINDERGARTEN PROBLEM SOLVING,” 2019)
The concept of problem-solving occurs in many different appearances and scopes. Some problems can be rather minor and arise in an incidental manner from activities or on the other hand, problems can be a part of a major project.
So why is problem-solving important?
According to Gifford, Piaget (1973) and Vygotsky (1978) have encouraged problem-solving techniques as an important ‘vehicle for learning’. They have highlighted the collaborative, as well as guided problem-solving as a significant technique. Children need to learn how to connect the skills they already know to new situations, to overcome current and future difficulties they come across. When problem-solving, children can be encouraged in making new connections with their current knowledge and this may moreover provide motivation for learning. An advantage of the problem-solving technique involves, all the main cognitive learning processes (attention, language, learning, memory, perception, and thought) in visualizing solutions, checking for possible errors, and in all context given instruction along with talking and reflecting. Problem-solving is important since it comprises metacognition – a higher-order thinking which enables one’s cognitive process by understanding, analyzing, and controlling it (Definition of Metacognition, n.d.) – used in evaluating strategies and solutions (Gifford, 2005).
Problem-solving skills can stimulate a higher level of thinking, including an extended analysis of the problems, a synthesis of important ideas, and the use of creativity when unfamiliar solutions are found. Furthermore, problem-solving usually involves some significant emotional and social learning where successful problem-solving may enhance a child’s self-esteem and may help the child grow and develop a ‘mastery orientation’. Co-operative problem-solving may help form good relationships by giving emotional and cognitive support, which have the need for social skills. Some examples of social skills are: gaining entry, both taking and giving advice, and most importantly resolving disagreements. By definition, problem-solving is difficult to pursue and may sometimes threaten a child’s – or even an adult’s – self-esteem. Thus, a teacher’s help and sympathy play a key role in fostering an encouraging and supportive climate for problem-solving in the classroom (Gifford, 2005).
Some successful problem-solving strategies include:
- Comprehending the problem, looking at the problem as a whole, checking if the children have understood the problem by asking them questions and going through it.
- Preparing, planning, and predicting the outcomes of the solution. For example, when playing with blocks, gather them all together before starting to build.
- Monitoring the procedure and progress towards the target. For example, checking that all blocks fit in a box.
- Be efficient by trying all possibilities -without repeating – methodically instead of randomly trying. For example, separate the shapes of a puzzle into two categories (or more): those the children have already tried and those not tried yet.
- Trying different options of approaches and evaluating distinct strategies. For example, trying the different arrangements of each block/shape.
- Improving and reefing a solution. For example, by solving a puzzle for a second time using fewer moves and being quicker.
All the above strategies involve, among other things, the reflection and awareness of the thinking process. Teachers can advise children to use the above strategies by helping them model these strategies as well as encourage them to talk and compare the different methods they used in the solution. Teachers could also, recommend to children, to ‘prepare’ a list of alternative methods to select from, conveying a range of expertise. In addition, children need to adopt the confidence of being flexible and familiar with working on the solution of a problem while, using everything they know.
How can teachers help? In general, the notion of ‘Problem-solving’ is considered to be difficult to teach. However, children can be taught on how to use these strategies, which usually involve mathematical ideas. For example, kindergarten teachers (or adults in general), can teach children to check their answers using counting and can even provide them with the puzzle- and computer game-based strategies. An example that supports problem-solving is scaffolding (a process through which teachers add support for students to enhance learning and assist them with the difficultness of the task): this covers the provision of support depending on a child’s responses, for example, breaking down the problem in smaller steps and helping the children draw attention to the key features. Questioning is considered as a significant strategy to help focus a child’s attention, but more exquisite strategies, such as making comments or looking can be also effective. Furthermore, asking the children to describe (talk about), and to demonstrate the steps of what they have done, may help them examine and evaluate the problem. Researchers have found that when a teacher encourages children to check their answers – their steps – means that later on, they would do this themselves. Gifford suggests that it is useful to ask older children some ‘self-organizing’ questions, of which children could use as examples and base their questions on them. An example of the different stages of a problem could be:
| Getting to grips: | What are we trying to do? |
| Connecting to previous experience: | Have we done anything like this before? |
| Planning: | What do we need? |
| Considering alternative methods: | Is there another way? |
| Monitoring progress: | How does it look so far? |
| Evaluating solutions: | Does it work? |
| How can we check? | |
| Could we make it even better? |
Adults who encourage the curious and questioning behavior in children, suggest that demonstrating attitudes may be equally important as the teaching strategies. Children can pursue and become confident in problem-solving, with the help of teachers who recognize the difficulties of problem-solving but can also establish the determination that could help them.
Different types of problem-solving provide a variety of learning experiences for the children, and can also implement an effective teaching strategy that evaluates and clarifies all misconceptions and increases children’s understanding.
Prospects for mathematical problem-solving:
Adult-initiated:
- Preparation – examining that there are sufficient items for everyone, e.g., brushes, puzzles
- Share – examining that all children have an equal amount
- Tidy up – organizing the storage and examining that nothing has been lost
- Gardening – arranging plants and bulbs, and predicting how fast they grow
- Vote – for stories, songs, games and in general vote for the activities
- Plan and set up – a wild garden or new role-play area
- Communication – plans, measurements, invitations with times and maps
Child-initiated:
- Construction plays and model-making materials – finding similar shapes, fitting things together, checking sizes
- Pattern-making materials – generating patterns and setting up rules, such as using shape properties, movements, and positions
- Drawing and picture-making materials – creating shapes to represent things
- Open-ended role-play activities – the ‘whatever you want it to be place’, for children to construct their own scenarios
- Mathematical utilities for children to use while playing – for example, DIY calendars for making appointments, calculators for working out prices, scales for weighing a baby, etc.
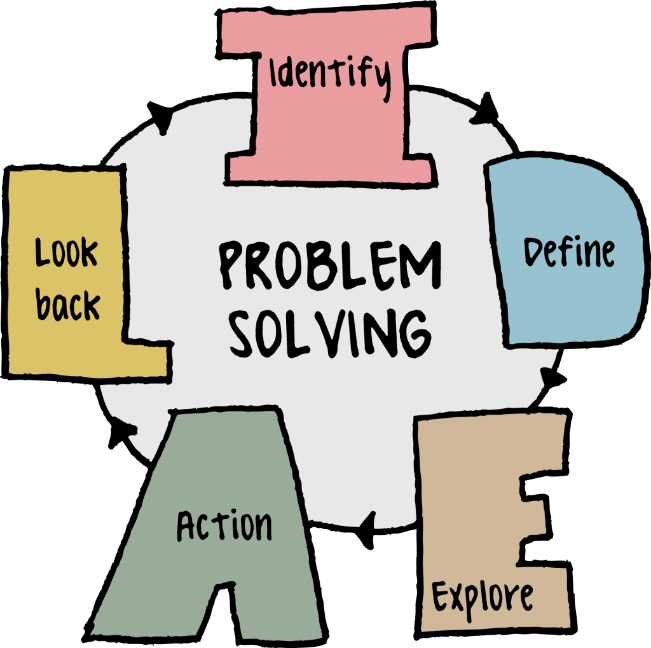
George Polya’s book ‘How to solve it, (1945)’, describes how students can adopt problem-solving skills. Even though his advice is directed to older students (high school and university students), it can be adapted and applied to younger kindergarten students. Polya gives four steps that a student should follow when solving a problem:
- Understanding the problem; this first step is regularly neglected as it is considered too obvious by students. Polya advises teachers to use some of the following questions to help direct the students in the correct path of understanding the problem. Some questions are:
- What are you asked to find?
- Can you define and describe the problem in your own words?
- Can you think of a diagram or picture that might be able help you comprehend the problem?
If children are unclear as to what needs to be solved, then they will most probably get the wrong answer. Understanding the problem is the most important step and in general, more emphasis should be given to this step.
- Devising the plan; This is a step that is in sync with the policy of encouraging the representation of thinking. This step is the plan, or a translation of the problem in the form of an equation, a diagram, a chart that will help in the process of solving the problem.
- Carrying out the plan; This is the step where you solve the plan of the previous step. It can be considered as an easier step than the previous one since all that needs to be done is to solve the equation of step 2.
- Looking back (review/extend); When problem-solving, it is good to look back and check if you used all the information and review that the answer makes sense. Doing this step can help you predict a distinct strategy that can be used to solve future problems.
By understanding these four steps at a young age, may give students an advantage when solving a problem at a later age (Polya, 1945). To conclude, problem-solving can be considered as the foundation in young children’s learning process. Problem-solving must be respected, provided for, encouraged, and sustained in the kindergarten classroom. There are multiple opportunities for problem-solving which may occur in a child’s everyday life. In section 5.3 we will elaborate on how, by using the child’s cognitive, social, emotional as well as movement experiences facilitate problem-solving and promotes approaches useful in the enduring learning process (Britz, 1993).
5.3 – Teach children to view and describe their world mathematically
In recent years, there has been a major advancement in the teaching of ‘thinking skills’. The notion of ‘thinking skills’ has been identified as introducing the ‘reasoning, inquiry, and creativeness’ of thinking skills. Inquiry combines prediction and creative thinking skills which covers the ‘search’ for various innovative conclusions. Teachers can use this process by encouraging children to ‘think aloud’, but further to embolden and stimulate the methods they have used for solving a problem (Gifford, 2005).
It’s more important to demonstrate the logic of math than to memorize rules
Alice P. Wakefield
While school teachers try to teach children a mathematical expression or problem, they usually provide them the correct answer before children make an effort in thinking what the answer might be. Such teachers, eliminate the need for reflection, which can be considered as the one that ‘underlies lasting learning’. Teachers should establish three teaching strategies that will help reinforce a student’s thinking. These three teaching strategies are:
‘Encourage your students to think’. Although this principle does not sound unreasonable, most teachers usually pass over it. Instead of encouraging each and every student to develop their unique way of thinking – their number sense – every child is expected to solve a mathematical problem in the same way. However, by simply asking the children if they agree with their fellow students’ answers or how they can solve the problem differently, the teacher encourages them to challenge their thinking.
Moving on to ‘encouraging children to think about thinking’. To support the learning of young children in kindergarten, teachers should encourage their students to think about their thinking. In other words, to help them form a concept of how they ended up with that specific answer. By challenging a kindergarten child to think about their thinking, you help them become more skilled and will therefore be used at doing it. Teachers can start their questions with words such as, “How”; “What”; “Why”; “Which”. One even better idea can be to advise them to work in teams. Children will compare their answers and possibly different methods used, rethink their solutions, and might even defend their logic.
Lastly, ‘encourage representations of thinking’. Children should know how to represent their thinking with words, pictures, or symbols. Encouraging the children to reflect and represent their thinking in the classroom will therefore lead to even more thinking and more thinking about thinking.
These three principles can support a more complicated, and at the same time a more practical mental activity. Nonetheless, it seems that an approach that requires thinking is considered a more challenging approach by teachers, rather than learning the textbook by heart. Just as a child that learns to follow specific rules to get to the correct answers does not grow in an understanding of math logic, teachers who follow a specific “recipe” to meet math targets do not grow in the understanding of teaching and learning (Wakefield, 2001)!
Children, teens, and adults, all experience in a unique way, conveying a divergence in the ways we learn best. A teacher’s way of handling their students can be impacted by understanding all four different types of learning styles and adapting to an individual’s learning. If an individual’s learning style has not been activated, this individual might end up lagging behind the rest of his/her classmates. There are four different learning styles: visual learners, auditory learners, reading/writing learners, and kinesthetic learners. The majority of students usually represent more than one learning style each, however, a teacher should adjust the lesson in such a way so that all different learning styles are covered (Malvik, 2020). Furthermore, children have a unique preference in the way they learn: some by hearing, some by doing, others by seeing, some children by reading and others by asking questions. However, all children have one thing in common: all learn best when they can combine objects and topics that find more interesting (4 Different Learning Styles You Should Know, n.d.). Planning a lesson that meets all the aforementioned types of learners can be considered easier while children are still in kindergarten.
Having all the above in mind, teachers could use this information to teach children how to view and describe their world in a mathematical way. Children could be encouraged to describe in their own words and language, the mathematics they observe and experience in the real world. Research has shown that by applying math concepts to real-world situations during children’s play time at school, helps them establish a better understanding of the concepts they are learning. The above recommendations can be implemented using the following steps:
- Encouraging kindergarten children to represent mathematical concepts, solutions or processes, using informal methods. This step can be completed by connecting mathematical concepts to children’s experiences using terms and comparisons that are recognized by the children.
- Helping children link their experiences and informal knowledge to the formal math symbols, procedures and vocabulary. Teacher may begin to introduce some formal mathematical concepts, just after children seem to be comfortable with the informal representation of the math concepts. Teachers may proceed by connecting informal and formal representations together.
- Using open-ended questions in encouraging children to instantly apply their math knowledge. Questions starting with “what”, “why”, “how”, inspire children to think about the informal and formal math vocabulary and concepts.
- Encouraging children to identify mathematics in everyday situations and talk about it. A child’s math knowledge can be strengthened by giving them opportunities to connect the math concepts learned in class to the real world (Teaching Math to Young Children, 2013).
- To conclude, mathematics is a subject that attracts children’s interest only when children themselves comprehend that mathematics can be considered as a tool that can be used in solving real-world problems. The goal of the recreaMATHS approach is for teachers to transfer to the kindergarten children this problem-solving way of thinking. Once teachers understand that an international low performance of children in mathematics reflects the need for a ‘recreation’ in the approach used in teaching mathematical concepts, then there will be an excess in the children’s mathematical skills. It is advised, that the approach will be distinct from the traditional approach of the teaching and learning of mathematics to attract the interest of as many children as possible (Gifford, 2005). As mentioned above, one of the best ways for teachers to “mathematize” kindergarten children, is to use mathematical concepts in their daily routine. For example, as games or in a different entertaining way to solve a problem. To sum up, attitude matters, therefore, it is suggested that teachers encourage children to believe in success (Pellissier, 2015).
To conclude, mathematics is a subject that attracts children’s interest only when children themselves comprehend that mathematics can be considered as a tool that can be used in solving real-world problems. The goal of the recreaMATHS approach is for teachers to transfer to the kindergarten children this problem-solving way of thinking. Once teachers understand that an international low performance of children in mathematics reflects the need for a ‘recreation’ in the approach used in teaching mathematical concepts, then there will be an excess in the children’s mathematical skills. It is advised, that the approach will be distinct from the traditional approach of the teaching and learning of mathematics to attract the interest of as many children as possible (Gifford, 2005). As mentioned above, one of the best ways for teachers to “mathematize” kindergarten children, is to use mathematical concepts in their daily routine. For example, as games or in a different entertaining way to solve a problem. To sum up, attitude matters, therefore, it is suggested that teachers encourage children to believe in success (Pellissier, 2015).
Math is the language of logic
Dr. Jie-Qi Chen
116 References:
4 Different Learning Styles You Should Know: The VARK Model. (n.d.). Retrieved October 29, 2020, from https://educationonline.ku.edu/community/4-different-learning-styles-to-know
Abba, G. (1995). Ruolo del materiale didattico nel processo di apprendimento e integrazione del non vedente in età evolutiva. Tiflologia per l’integrazione, 5 (3), supplem., 34-36.
Anthony, G., & Walshaw, M. (n.d.). Effective pedagogy in mathematics. 32.
Asha K., Jitendra K. H., Beck M., “L’uso degli schemi visivi per la risoluzione dei problemi matematici, in Difficoltà di apprendimento”, Vol. 8, n. 1, Lehigh University, Bethlehem, 2002.
Balakrishnan, C. (2008). TEACHING SECONDARY SCHOOL MATHEMATICS THROUGH STORYTELLING. 306.
Bavelier D, Tomann A, Hutton C, Mitchell T, Corina D, Liu G, et al. (2000) Visual attention to the periphery is enhanced in congenitally deaf individuals. Journal of Neuroscience 20:1–6.
Best Digital Book in Maths/Sciences 2018 https://innotechtoday.com/digital-book-world-2018/
Britz, J. (1993) Problem Solving in Early Childhood Classrooms. https://files.eric.ed.gov/fulltext/ED355040.pdf
Candiotta Giusla mateeppina, “la matematica per i sordi”, relatore Enrico Dolza. – Tesi dattiloscritta. – Torino: Università degli studi, 2015-2016.
Chiara Nanni , Enrica Partesana and Daniela Rocca “Early Identification and Strengthening of Learning Difficulties A Project of Collaboration between School and Neuropsychiatry Service”, Edizione Erickson, DIS Vol. 1, Issue 1, January 2020
Culture and the arts. (2019). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Wikipedia:Contents/Culture_and_the_arts&oldid=926544104
D. Fabbretti, E. Tomasuolo, “Scrittura e sordità” Carrocci, Roma, 2006
d’Entremont, Y. (2015). Linking Mathematics, Culture and Community. Procedia – Social and Behavioral Sciences, 174, 2818–2824. https://doi.org/10.1016/j.sbspro.2015.01.973
Davide Antognazza and Silvia Sbaragli “The Influence of the Teacher’s Attitude over the Students’ Commitment Mathematics Education Case “, Edizione Erickson, DIS Vol. 1, Issue 1, January 2020
Definition of metacognition. (n.d.). Www.Dictionary.Com. Retrieved October 26, 2020, from https://www.dictionary.com/browse/metacognition
Dooley, T., Dunphy, E., Shiel, G., Butler, W. D., Corcoran, D., Farrell, T., NicMhuirí, S., O’Connor, M., & Travers, J. (n.d.). Mathematics in Early Childhood and Primary Education (3-8 years). 164.
Drew, C. (2020). The 5 Key Features of Child Initiated Play (2020). Helpful Professor. https://helpfulprofessor.com/child-initiated-play/
European Math Museums Questionnaire
Fermat Science: https://www.fermat-science.com/
Finkel, D. (2015, June 13). 5 principles of extraordinary math teaching. Math for Love. https://mathforlove.com/2015/06/5-principles-of-extraordinary-math-teaching/
Finkel, D. (2016, May 11). Hate Math? Make It Fun With Picture Books, Board Games and More. Math for Love. https://mathforlove.com/press/hate-math-make-it-fun-with-picture-books-board-games-and-more/
Francesco Sella, Daniela Lucangeli and Marco Zorzi “The Mastering of the Cardinality Principle in a Sample of Italian Preschool Children” Edizione Erickson, DIS Vol. 1, Issue 2, May 2020
Frye, D., Baroody, A., Burchinal, M., Carver, S., Jordan, N., & McDowell, J. (2013). Teaching Math to Young Children. The Institute of Education Sciences (IES), 1–152. https://ies.ed.gov/ncee/wwc/Docs/PracticeGuide/early_math_pg_111313.pdf
Gifford, S. (2005). Teaching Mathematics 3-5: Developing Learning in the Foundation Stage. http://eds.a.ebscohost.com/eds/ebookviewer/ebook/bmxlYmtfXzIzMzkzM19fQU41?sid=f1519a5c-1edb-4669-8a83-c8f4a4142877@sdc-v-sessmgr01&vid=0&format=EB&rid=1
Ginsburg, H. P., Inoue, N. & Seo, K. H. (1999). Young children doing mathematics: Observations of everyday activities. In J. Copely (Ed.), Mathematics in the early years (pp.88–99). Reston,VA: NCTM
Giulia Franconi and Cesare Cornoldi, “A Study on the Change of the Relationship between Mathematics and Metacognition in Different School Levels” Edizione Erickson, DIS Vol. 1, Issue 1, January 2020
How play is structured in early years settings to promote development. (n.d.). 6.
How to teach kindergarten and preschool math. (2019, June 24). Kindergarten Lessons. https://www.kindergarten-lessons.com/kindergarten-and-preschool-math/
Instructional Research Group. (2008, January). Mathematics Instruction for Students with Learning Disabilities or Difficulty Learning Mathematics: A Guide for Teachers. Center on Instruction. https://www.researchgate.net/publication/234623037_Mathematics_Instruction_for_Students_with_Learning_Disabilities_or_Difficulty_Learning_Mathematics_A_Guide_for_Teachers
Jayanthi, Madhavi & Gersten, Russell & Baker, Scott. (2008). Mathematics Instruction for Students with Learning Disabilities or Difficulty Learning Mathematics: A Guide for Teachers. Center on Instruction.
Johansson, M. (2015). Perceptions of mathematics in preschool “-now we have a way of talking about the mathematics that we can work with.”
Jones, C. (2009). Interdisciplinary Approach: Advantages, Disadvantages, and the Future Benefits of Interdisciplinary Studies.
Khasnabis, C., Motsch, K. H., Achu, K., Jubah, K. A., Brodtkorb, S., Chervin, P., Coleridge, P., Davies, M., Deepak, S., Eklindh, K., Goerdt, A., Greer, C., Heinicke-Motsch, K., Hooper, D., Ilagan, V. B., Jessup, N., Khasnabis, C., Mulligan, D., Murray, B., … Lander, T. (2010). Non-formal education. In Community-Based Rehabilitation: CBR Guidelines. World Health Organization. https://www.ncbi.nlm.nih.gov/books/NBK310920/
KINDERGARTEN PROBLEM SOLVING. (2019, February 27). Kindergarten Lessons. https://www.kindergarten-lessons.com/kindergarten_problem_solving/
L’ Europe mathématique/Mathematical Europe: Histoires, mythes, identités publié par Catherine Goldstein, Jeremy Gray, Jim Ritter
Le Point Hors-Série, La Méthode Singapour, December 2017
Les Défis de l’enseignement des mathématiques dans l’éducation de base, Michèle Artigue, Unesco report, 2011
Making the Connection between Culture and Mathematics Northwestern University | School of Education & Social Policy. (n.d.). Retrieved December 18, 2020, from https://www.sesp.northwestern.edu/news-center/inquiry/2009-spring/making-the-connection.html
Malvik, C. (2020). 4 Types of Learning Styles: How to Accommodate a Diverse Group of Students. https://www.rasmussen.edu/degrees/education/blog/types-of-learning-styles/
Maria Grazia Palermo, “Matematica e scienze con l’alunno sordo : teaching mathematics and science of to the deaf students”; relatore Enrico Dolza. – Tesi dattiloscritta. – Torino : Università degli studi, 2015 (TESI 136).
Mathematics in Early Childhood and Primary Education (3-8 years), NCCA,
Mathematikum museum: https://www.mathematikum.de/
Mmaca museum: https://mmaca.cat/
Mok, O. N. A. (2011). Non-formal learning: Clarification of the concept and its application in music learning. Australian Journal of Music Education, 1, 11–15.
Navet museum: https://www.navet.com/
Neculae Dinuță – Methodical aspects regarding the interdisciplinary approach of mathematical contents in preschool education. Procedia – Social and Behavioral Sciences 180 ( 2015 ) 780 – 787
NMC HorizonReport: 2017 Higher Education Edition
Non-formal education. (1999). https://assembly.coe.int/nw/xml/XRef/X2H-Xref-ViewHTML.asp?FileID=8807&lang=EN
Non-formal education. (2020, June 22). http://uis.unesco.org/en/glossary-term/non-formal-education
Observation Cooperation Information Museums: https://ocim.fr/2020/12/approches-sociales-et-inclusives-des-musees-et-des-lieux-de-culture-scientifique/
Oldridge, M. (2019). The Playful Approach to Math. Edutopia. https://www.edutopia.org/article/playful-approach-math
Papadakis, S., Kalogiannakis, M., & Zaranis, N. (2016). Improving Mathematics Teaching in Kindergarten with Realistic Mathematical Education. Early Childhood Education Journal, 45(3), 369–378.
Pellissier, H. (2015). Why early math is just as important as early reading. Parenting. https://www.greatschools.org/gk/articles/early-math-equals-future-success/
Pigliacampo R.,” Lingua e Linguaggio nel sordo, analisi e problemi di una lingua visivo-manuale”, Armando Editore, Roma, 1998.
Pourquoi l’école a-t-elle enseigné le comptage-numérotage pendant près de 30 années ?, Rémi Brissiaud, september 2014
Press article on maths museums: https://lepetitjournal.com/francfort/a-voir-a-faire/mathematikum-le-premier-musee-interactif-des-mathematiques-giessen-attire-les-visiteurs-77890
Rosy Luca, “Insegnare matematica ad allievi con disabilità acustica = teaching mathematics for deaf student”, rel. Cecilia Maria Marchisio. – Tesi dattiloscritta. – Torino : Università degli Studi, PAS Piemonte – a.a. 2013-2014 (TESI 119).
Samarapungavan, Patrick, Mantzicopoulos, A. H. P. (2011). What Kindergarten Students Learn in Inquiry-Based Science Classrooms. Taylor & Francis Group, 416–470. https://doi.org/10.1080/07370008.2011.608027
Seel, N. M. (2012). Action Schemas. In N. M. Seel (Ed.), Encyclopedia of the Sciences of Learning (pp. 73–75). Springer US. https://doi.org/10.1007/978-1-4419-1428-6_356
Sensorineural Hearing Loss Occurs in the Cochlea | MED-EL, https://www.youtube.com/watch?v=EfzvT_WR0x4.
Simonetta Maragna, “ Una scuola oltre le parole : educare il bambino sordo alla lingua parlata e scritta : con esempi di unità didattica” ; presentazione di Virginia Volterra. – Milano : F. Angeli, 2003 (Cap. 4: Le unità didattiche. Area Logico-matematica).
Soares, N., Evans, T., & Patel, D. R. (2018). Specific learning disability in mathematics: a comprehensive review. Translational Pediatrics, 7(1), 48–62. https://doi.org/10.21037/tp.2017.08.03
Spiteri, M. (2016, August 18). The benefits of non-formal learning [Text]. EPALE – European Commission. https://epale.ec.europa.eu/en/blog/benefits-non-formal-learning
St Patrick’s College, Charles Sturt University, & Educational Research Center. (2014a). Mathematics in Early Childhood and Primary Education (3–8 years) Definitions, Theories, Development and Progression (No. 17). National Council for Curriculum and Assessment.
St Patrick’s College, Charles Sturt University, & Educational Research Center. (2014b). Mathematics in Early Childhood and Primary Education (3–8 years) Teaching and Learning (No. 18). National Council for Curriculum and Assessment.
Subitising and Early Number Sense in Early Years Children—Yellow Door. (n.d.). Retrieved October 27, 2020, from https://www.yellow-door.net/blog/what-is-subitising/
Teaching Math to Young Children. (2013). 165.
Teresa Ferraiuolo and Rosanna Coseglia, ”Playing with Numbers and Letters An Enhancement Experience in an Inclusive Context” Edizione Erickson, DIS Vol. 1, Issue 1, January 2020
Terezinha Nunes, “Teaching mathematics to deaf children” – London and Philadelphia: Whurr, 2004.
Tiziana Raso, “Metodologie didattiche per l’insegnamento della matematica ai sordi : didactic methods for teaching mathematics to deaf students”; relatore Enrico Dolza. – Tesi dattiloscritta. – Torino : Università degli studi, 2015. (TESI 138).
Tran, C., Smith, B., & Buschkuehl, M. (2017). Support of mathematical thinking through embodied cognition: Nondigital and digital approaches. Cognitive Research: Principles and Implications, 2(1), 16. https://doi.org/10.1186/s41235-017-0053-8
Tudge, J., & Doucet, F. (2004). Early mathematical experiences: Observing young black and white children’s everyday activities. Early Childhood Research Quarterly, 19(1), 21–39.
UDL: The UDL Guidelines. (2021, April 9). The UDL Guidelines. https://udlguidelines.cast.org.
Una app dedicata ai bambini ciechi per imparare la matematica : https://www.superabile.it/cs/superabile/istruzione/una-app-dedicata-ai-bambini-ciechi-per-imparare-la-matematica.html.
Understanding teaching professionals’ digital competence: What do PIAAC and TALIS reveal about technology-related skills, attitudes, and knowledge?, R. Hamalainen et al., 2020
Valentina Franceschina “Il bambino non vedente e la matematica: quali strumenti è opportuno utilizzare per facilitare questo apprendimento?” tesi di laurea in scienze della educazione.
Valentina Mengoni and Laura Maria Castagna, “Comparison between Reading Performances of Children with Specific Learning Disabilities and Learning Difficulties by Using Times New Roman and EasyReading Writing Font” Edizione Erickson, DIS Vol. 1, Issue 2, May 2020
Vodopivec, J. (in press). COOPERATIVE LEARNING AND SUPPORT STRATEGIES IN THE KINDERGARTEN. Metodički Obzori.
Vygotsky L. S., “Pensiero e linguaggio”, a cura di Costa A., Giunti, Firenze, 1966.Ø M. C. Caselli, S. Maragna, V. Volterra, “Linguaggio e sordità”, il Mulino, 2006
Wakefield, A. P. (2001). It’s more importantto demonstratethe logic of math than to memorize rules. 5.
What are strategies for teaching a student with a math-related learning disability? | DO-IT. (n.d.). What Are Strategies for Teaching a Student with a Math-Related Learning Disability? Retrieved January 12, 2021, from https://www.washington.edu/doit/what-are-strategies-teaching-student-math-related-learning-disability
What are typical challenges students with math-related learning disabilities face? | DO-IT. (n.d.). What Are Typical Challenges Students with Math-Related Learning Disabilities Face? Retrieved January 14, 2021, from https://www.washington.edu/doit/what-are-typical-challenges-students-math-related-learning-disabilities-face?323=
What is a holistic approach? – Principles for effective support. (n.d.). Retrieved October 27, 2020, from https://www.health.nsw.gov.au/mentalhealth/psychosocial/principles/Pages/holistic.aspx
What Is Culture? Definition, Meaning and Examples | Live Science. (n.d.). Retrieved November 13, 2020, from https://www.livescience.com/21478-what-is-culture-definition-of-culture.html
What is non formal education and why it is important. (2018, September 18). Dothegap / Sube Tu Experiencia. Descubre Otras Afines. Conecta. https://dothegap.com/blog/en/what-is-non-formal-education-and-why-it-is-important/
What is non-formal education? (2015). https://infed.org/mobi/what-is-non-formal-education/
What’s Dyscalculia? (n.d.). What’s Dyscalculia? Retrieved January 15, 2021, from https://www.dyscalculia.org/dyscalculia/what-s-dyscalculia
Yeo, D. (2003). Dyslexia, Dyspraxia and Mathematics (1st ed.). Wiley.
Zisopoulou, E. (2019). Collaborative learning in kindergarten: Challenge or reality? Erken Çocukluk Çalışmaları Dergisi, 3(2), 335–351. https://doi.org/10.24130/eccd-jecs.1967201932113