From playing with mathematics to admiring it

At Recreamaths, we believe that learning math should be fun. Showing children that solving mathematics problems can be likened to a game is without doubt an effective way of ensuring they develop strong numeracy skills for the future.

There is however another way of encouraging children to engage more fully into mathematics, and that is less common than the one mentioned above. That is allowing children to observe for themselves the beauty of mathematics. Because yes, mathematics is not only fun, but it is also beautiful.

Mathematical beauty in visual compositions: symmetry and proportion

Different people might understand differently the idea of the beauty of mathematics. One thing that usually comes to mind is the fact that mathematical concepts are found everywhere in the world, and that such concepts don’t just structure the world in the way they function, but they do so also in the way they look. In other words, they structure them visually, and do so all the while infusing them with a sense of balance or equilibrium, or in other words, of beauty.

Indeed, equilibrium is highly linked to beauty through the concept of harmony: equilibrium gives a composition – whether visual, or musical, or in some other medium – a sense of harmony which we humans perceive as beautiful. Symmetrical compositions for example have been represented and admired for centuries and across civilisations for their beauty. This is the case whether they are structured along central or axial symmetry on a two-dimensional plane:

Ornamentation of the main entrance; Mir-i-Arab madrasa; Po-i-Kalyan ensemble. Bukhara, Uzbekistan

Symmetry can also arise in three-dimensional planes. It can manifest itself in volumes when a volume cut in half produces two identical volumes as in radial symmetry, or when a volume is itself made of identical smaller volumes, as in fractals. Such symmetrical volumes again are considered pleasant to the eye, but also the mind. In fact Plato considered the sphere – the radial volume by excellence since any two halves are identical – the “most symmetrical and homogeneous form that existed. And therefore the most beautiful and perfect form of all.”

Romanesco cauliflower

But an even earlier mathematical concept than symmetry – that of proportion namely – also takes an important part in characterising the notion of beauty. (After all, the Ancient Greek word summetria used to refer to comparable proportions, before coming to refer to the visual principle it refers to today.) And here again, mathematics is the language to define, characterise and structure harmony and beauty.

The golden ratio is often cited as the mathematical proportion that gives a sense of harmony and beauty in visual compositions – and ones that might occurr both naturally and artificially: from the proportions to the human body and the nautilus, to those of the Parthenon and the Pyramids. It is worth noting that the golden ratio goes as far as to extend to natural phenomena as well such as the rate at which the leaves of a tree grow for instance.

Nautilus shell

Mathematical beauty in the practice of mathematics itself

But while some people might think of symmetry and proportion as the sole – or at least the main – manifestations of the beauty of mathematics, others might have something else in mind. Mathematicians notably, but also anybody who enjoys mathematical reflection and problem solving, might revel in mathematical beauty when they engage in these two very activities.

Indeed, many people admire the beauty of mathematics that occurs on various occasions and notably these two: 1) in the method, when solving a complex problem with a simple – but logical and sufficient – solution ; 2) in the result, when arriving upon a seemingly surprising conclusion from a quite distant set of premises.

Examples of the former might be the many theorems and mathematical formulas we memorise in schools, every one of which are the result of many different attempts to prove the same end result albeit in more numerous steps and more lengthy terms.

Examples of the latter might be identities such as Euler’s identity – which Feynman referred to as a “jewel” and “the most remarkable formula in mathematics – which establishes a connection made of unexpectedly basic arithmetic operations (addition, exponiention and multiplication) between such fundamental mathematical constants (π, i and e):

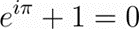
But mathematician Serge Lang insists that one has to exercise and understand mathematics to see its beauty – that it cannot be explained – and also that such beauty is best observed in pure rather than applied mathematics. It all comes down to seeing mathematics not only as a means to an end, not only as a tool to do physics, architecture, or accounting, but as something greater than the sum of its parts, greater than the mere manipulation of numbers or shapes. Just like music is not just a collection of notes, mathematics is not just numbers and equations. (5)

Sheet music

He goes on to explain this parallel with these words:

“When you write a musical piece, you use notes, but the notes are not the music. To read a piece of music from the written text is not a substitute for hearing the piece in Carnegie Hall or elsewhere. Logic is the hygiene of mathematics, just as grammar and syntax are the hygiene of language—and even then! “Under the bam, under the boo, under the bamboo tree . . .”, there isn’t any grammar. The essential thing in Shakespeare, or Goethe, is not grammar or syntax. It is the poetry, the musical effect of words, poetic allusions, aesthetic impressionism, and many other things. But whereas the beauty of poetry pales under translation, the beauty of mathematics is invariant under linguistic transformations.” (18)

So when encouraging your children to do mathematics, don’t just try to convince them it’s fun, try to show them as well that mathematics is beautiful – more so than literature and music in some ways – and that to appreciate this beauty, they will first have to understand it.

Sources

  • Lang, Serge. The beauty of doing mathematics: Three public dialogues. Springer Science & Business Media, 1985.
  • Museu do Amanhã. The hidden beauty of mathematics. Google Arts & Culture. <https://artsandculture.google.com/story/XAVxHxByw1SoIw> accessed on December 11th 2022.

Media